Die Integralrechnung ist ein Zweig der Infinitesimalrechnung und bildet mit der Differentialrechnung die mathematische Analysis. Sie ist aus der Aufgabe entstanden, Flächeninhalte oder Volumina zu berechnen, die durch gekrümmte Linien bzw. Flächen begrenzt sind. Unter dem Oberbegriff Integral werden das unbestimmte und das bestimmte Integral einer Funktion zusammengefasst. Die Berechnung von Integralen heißt Integration.

• Das bestimmte Integral einer Funktion ${\displaystyle f}$ ergibt eine Zahl. Ist ${\displaystyle f}$ eine reelle Funktion einer reellen Variablen ${\displaystyle x}$, die im ${\displaystyle xy-}$Koordinatensystem in einem Intervall von ${\displaystyle a\leq x\leq b}$ durch einen Graphen dargestellt ist, dann gibt das bestimmte Integral den Inhalt der Fläche an, die in diesem Intervall zwischen dem Graphen und der ${\displaystyle x}$-Achse liegt. ${\displaystyle a}$ und ${\displaystyle b}$ werden als Integrationsgrenzen bezeichnet. Falls Flächenstücke unterhalb der ${\displaystyle x}$-Achse vorkommen, werden diese hierbei negativ gezählt. Diese Vorzeichenkonvention wird gewählt, damit das bestimmte Integral eine lineare Abbildung vom Raum der Funktionen in den Zahlenraum ist, was sowohl für theoretische Überlegungen als auch für konkrete Berechnungen eine zentrale Eigenschaft des Integralbegriffs darstellt. Auch wird so sichergestellt, dass der Hauptsatz der Differential- und Integralrechnung gilt.
• Das unbestimmte Integral einer Funktion ${\displaystyle f}$ ist eine Funktion ${\displaystyle F}$ , deren erste Ableitung gerade die ursprüngliche Funktion ${\displaystyle f}$ ist. ${\displaystyle F}$ wird als Stammfunktion der Funktion ${\displaystyle f}$ bezeichnet. Addiert oder subtrahiert man zu ${\displaystyle F}$ eine beliebige Zahl, erhält man wieder eine Stammfunktion von ${\displaystyle f}$. Der Hauptsatz der Differential- und Integralrechnung gibt Auskunft darüber, wie mithilfe von unbestimmten Integralen bestimmte Integrale berechnet werden können.

Insoweit sind Integration und Differentiation Umkehrungen voneinander. Im Gegensatz zur Differentiation existiert für die Integration auch elementarer Funktionen aber kein einfacher und kein alle Fälle abdeckender Algorithmus. Integration erfordert trainiertes Raten, das Benutzen spezieller Umformungen (Integration durch Substitution, partielle Integration), Nachschlagen in einer Integraltafel oder das Verwenden spezieller Computer-Software. Oft erfolgt die Integration nur näherungsweise mittels numerischer Quadratur.

Flächenberechnungen werden seit der Antike untersucht. Im 5. Jahrhundert vor Christus entwickelte Eudoxos von Knidos nach einer Idee von Antiphon die Exhaustionsmethode, die darin besteht, Verhältnisse von Flächeninhalten mittels enthaltener oder überdeckender Polygone abzuschätzen. Er konnte durch diese Methode sowohl Flächeninhalte als auch Volumina einiger einfacher Körper bestimmen. Archimedes (287–212 v. Chr.) verbesserte diesen Ansatz, und so gelang ihm die exakte Bestimmung des Flächeninhalts einer von einem Parabelbogen und einer Sekante begrenzten Fläche ohne Rückgriff auf den Grenzwertbegriff, der damals noch nicht vorhanden war; dieses Ergebnis lässt sich leicht in das heute bekannte Integral einer quadratischen Funktion umformen. Zudem schätzte er das Verhältnis vom Umfang eines Kreises zu dessen Durchmesser, also die Kreiszahl ${\displaystyle \pi }$, als Wert zwischen ${\displaystyle \textstyle {3{\frac {10}{71}}}}$ und ${\displaystyle \textstyle {3{\frac {10}{70}}}}$ ab.

Diese Methode wurde auch im Mittelalter benutzt. Im 17. Jahrhundert stellte Bonaventura Francesco Cavalieri das Prinzip von Cavalieri auf, wonach zwei Körper das gleiche Volumen haben, wenn alle parallelen ebenen Schnittflächen den gleichen Flächeninhalt haben. Johannes Kepler benutzte in seinem Werk Astronomia Nova (1609) bei der Berechnung der Marsbahn Methoden, die heute als numerische Integration bezeichnet würden. Er versuchte ab 1612, den Rauminhalt von Weinfässern zu berechnen. 1615 veröffentlichte er die Stereometria Doliorum Vinariorum („Stereometrie der Weinfässer“), später auch als keplersche Fassregel bekannt.

Ende des 17. Jahrhunderts gelang es Isaac Newton und Gottfried Wilhelm Leibniz unabhängig voneinander, Kalküle zur Differentialrechnung zu entwickeln und so den Fundamentalsatz der Analysis zu entdecken (zur Entdeckungsgeschichte und zum Prioritätsstreit siehe den Artikel Infinitesimalrechnung; zum Integralzeichen und dessen Geschichte siehe Integralzeichen). Ihre Arbeiten erlaubten das Abstrahieren von rein geometrischer Vorstellung und werden deshalb als Beginn der Analysis betrachtet. Bekannt wurden sie vor allem durch das Buch des Adligen Guillaume François Antoine, Marquis de L’Hospital, der bei Johann I Bernoulli Privatunterricht nahm und darin dessen Forschung zur Analysis publizierte. Der Begriff Integral geht auf Johann Bernoulli zurück.

Im 19. Jahrhundert wurde die gesamte Analysis auf ein solideres Fundament gestellt. 1823 entwickelte Augustin-Louis Cauchy erstmals einen Integralbegriff, der den heutigen Ansprüchen an mathematische Strenge genügt. Später entstanden die Begriffe des Riemann-Integrals und des Lebesgue-Integrals. Schließlich folgte die Entwicklung der Maßtheorie Anfang des 20. Jahrhunderts.

„Kompakt“ bedeutet hier beschränkt und abgeschlossen, es werden also nur Funktionen auf Intervallen der Form ${\displaystyle [a,b]}$ betrachtet. Offene oder unbeschränkte Intervalle sind nicht zugelassen.

Ein Ziel der Integralrechnung ist die Berechnung von Flächeninhalten krummlinig begrenzter Bereiche der Ebene. In den meisten in der Praxis auftretenden Fällen sind derartige Flächen beschrieben durch zwei stetige Funktionen ${\displaystyle f,g}$ auf einem kompakten Intervall ${\displaystyle [a,b]}$, deren Graphen die Fläche begrenzen (linkes Bild).

: :

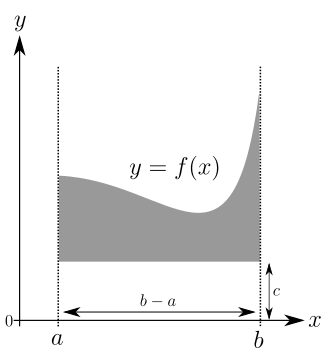
Der Flächeninhalt der grauen Fläche im linken Bild ist gleich der Differenz der grauen Bereiche in den beiden rechten Bildern. Es genügt also, sich auf den einfacheren Fall einer Fläche zu beschränken, die begrenzt wird von

• dem Graphen einer Funktion,
• zwei vertikalen Geraden ${\displaystyle x=a}$ und ${\displaystyle x=b}$
• sowie der ${\displaystyle x}$-Achse.

Auf Grund seiner fundamentalen Bedeutung erhält dieser Typ Flächeninhalt eine spezielle Bezeichnung:

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}$,

gelesen als Integral von ${\displaystyle a}$ bis ${\displaystyle b}$ von ${\displaystyle f}$ von ${\displaystyle x}$, ${\displaystyle \mathrm {d} x}$. Das Symbol ${\displaystyle \mathrm {d} x}$ steht für das Differential auf der ${\displaystyle x}$-Achse und gibt an, dass ${\displaystyle x}$ die Integrationsvariable ist, was vor allem bei Funktionen mit mehreren infragekommenden Symbolen von Variablen wichtig ist. Statt ${\displaystyle x}$ kann die Integrationsvariable im Differential und in der Funktion auch durch ein beliebiges anderes Symbol bezeichnet werden, abgesehen von denen für die Grenzen ${\displaystyle a}$ und ${\displaystyle b}$, zum Beispiel mit ${\displaystyle t}$ oder ${\displaystyle s}$. Der Wert des Integrals wird dadurch nicht geändert.

Verschiebt man den Graphen einer Funktion in Richtung der ${\displaystyle y}$-Achse um ein Stück ${\displaystyle c}$, so kommt zu der betrachteten Fläche ein Rechteck hinzu:

:

Das Integral ändert sich um den Flächeninhalt dieses Rechtecks der Breite ${\displaystyle b-a}$ und der Höhe ${\displaystyle c}$, in Formeln

${\displaystyle \int _{a}^{b}(f(x)+c)\,\mathrm {d} x=\int _{a}^{b}f(x)\,\mathrm {d} x+(b-a)\cdot c.}$

Betrachtet man eine stetige Funktion, deren Werte negativ sind, so kann man stets ein ${\displaystyle c\in \mathbb {R} }$ finden, sodass die Werte ${\displaystyle f(x)+c}$ im Intervall alle positiv sind (${\displaystyle c}$ muss größer als der Betrag des Minimums von ${\displaystyle f}$ in ${\displaystyle [a,b]}$ sein). Mit der vorhergehenden Überlegung erhält man

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=\int _{a}^{b}(f(x)+c)\,\mathrm {d} x-(b-a)\cdot c,}$

das heißt, das Integral von ${\displaystyle f}$ ist die Differenz der Flächeninhalte des weißen Bereichs in der Mitte und dem umgebenden Rechteck. Diese Differenz ist aber negativ, das heißt, soll die obige Formel für beliebige Funktionen korrekt sein, so muss man Flächen unterhalb der ${\displaystyle x}$-Achse negativ zählen. Man spricht deshalb von einem orientierten bzw. gerichteten Flächeninhalt.

Wenn eine oder mehrere Nullstellen im zu untersuchenden Intervall vorliegen, gibt das Integral nicht mehr den Flächeninhalt an, sondern die Summe aus den (positiven) Flächeninhalten der Teilflächen oberhalb der ${\displaystyle x}$-Achse und den (negativen) Flächeninhalten der Teilflächen unterhalb der ${\displaystyle x}$-Achse. Benötigt man in einem solchen Intervall die Fläche zwischen ${\displaystyle x}$-Achse und Graph der Funktion, muss das Integral an den Nullstellen aufgeteilt werden.

Es ist nicht einfach, den Begriff des Flächeninhaltes mathematisch präzise zu fassen. Im Laufe der Zeit wurden dafür verschiedene Konzepte entwickelt. Für die meisten Anwendungen sind deren Details jedoch unerheblich, da sie unter anderem auf der Klasse der stetigen Funktionen übereinstimmen. Im Folgenden werden einige Eigenschaften des Integrals aufgelistet, die oben motiviert wurden und unabhängig von der genauen Konstruktion für jedes Integral gelten. Außerdem legen sie das Integral stetiger Funktionen eindeutig fest.

Es seien ${\displaystyle a<b}$ reelle Zahlen, und es sei ${\displaystyle {\mathcal {F}}}$ ein Vektorraum von Funktionen ${\displaystyle [a,b]\to \mathbb {R} }$, der die stetigen Funktionen umfasst. Funktionen in ${\displaystyle {\mathcal {F}}}$ werden „integrierbar“ genannt. Dann ist ein Integral eine Abbildung

${\displaystyle {\mathcal {F}}\to \mathbb {R} ,}$

geschrieben

${\displaystyle f\mapsto \int _{a}^{b}f(x)\,\mathrm {d} x,}$

mit den folgenden Eigenschaften:

• Linearität: Für Funktionen ${\displaystyle f,g\in {\mathcal {F}}}$ und ${\displaystyle \lambda \in \mathbb {R} }$ gilt
  • ${\displaystyle \int _{a}^{b}(f(x)+g(x))\,\mathrm {d} x=\int _{a}^{b}f(x)\,\mathrm {d} x+\int _{a}^{b}g(x)\,\mathrm {d} x}$,
  • ${\displaystyle \int _{a}^{b}\lambda f(x)\,\mathrm {d} x=\lambda \cdot \int _{a}^{b}f(x)\,\mathrm {d} x}$.
• Monotonie: Ist ${\displaystyle f(x)\geq 0}$ für alle ${\displaystyle x\in [a,b]}$, so ist

  ${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x\geq 0.}$

• Integral der charakteristischen Funktion eines Intervalls: Ist ${\displaystyle I\subseteq [a,b]}$ ein Intervall und ist

${\displaystyle \chi _{I}(x)={\begin{cases}1\ ,&\mathrm {falls} \ x\in I\ ,\\0\ ,&\mathrm {falls} \ x\notin I\ ,\end{cases}}}$

so ist

${\displaystyle \int _{a}^{b}\chi _{I}(x)\,\mathrm {d} x}$

gleich der Länge des Intervalls ${\displaystyle I}$.

• Die reellen Zahlen ${\displaystyle a}$ und ${\displaystyle b}$ heißen Integrationsgrenzen. Sie können oberhalb und unterhalb des Integralzeichens oder seitlich vom Integralzeichen geschrieben werden:

${\displaystyle {\textstyle \int \limits _{a}^{b}}f(x)\,{\rm {d}}x}$     oder     ${\displaystyle \int \nolimits _{a}^{b}f(x)\,{\rm {d}}x}$

• Die zu integrierende Funktion ${\displaystyle f}$ heißt Integrand.
• Die Variable ${\displaystyle x}$ heißt Integrationsvariable. Ist ${\displaystyle x}$ die Integrationsvariable, so spricht man auch von Integration über ${\displaystyle x}$. Die Integrationsvariable ist austauschbar, statt

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}$

kann man genauso gut

${\displaystyle \int _{a}^{b}f(t)\,\mathrm {d} t}$ oder ${\displaystyle \int _{a}^{b}f(\xi )\,\mathrm {d} \xi }$

schreiben. In dem obigen Beispiel führt es zu unerwünschten Mehrdeutigkeiten, wenn man die Buchstaben ${\displaystyle a}$ oder ${\displaystyle b}$ verwendet, da sie bereits als Bezeichner für die Integrationsgrenzen fungieren. Daher sollte man darauf achten, dass das für die Integrationsvariable verwendete Zeichen nicht schon mit einer anderen Bedeutung belegt ist.

• Der Bestandteil ${\displaystyle \mathrm {d} x}$ wird Differential genannt, hat aber in diesem Kontext meist nur symbolische Bedeutung. Daher wird hier nicht versucht, ihn zu definieren. Am Differential liest man die Integrationsvariable ab.

Die symbolische Schreibweise von Integralen geht auf den Miterstbeschreiber der Differential- und Integralrechnung, Gottfried Wilhelm Leibniz, zurück. Das Integralzeichen ∫ ist aus dem Buchstaben langes s (ſ) für lateinisch summa abgeleitet. Die multiplikativ zu lesende Notation ${\displaystyle f(x)\,\mathrm {d} x}$ deutet an, wie sich das Integral – dem Riemann-Integral folgend – aus Streifen der Höhe ${\displaystyle f(x)}$ und der infinitesimalen Breite ${\displaystyle \mathrm {d} x}$ zusammensetzt.

In der theoretischen Physik wird aus pragmatischen Gründen oft eine leicht andere Schreibweise für Integrale benutzt (vor allem bei Mehrfachintegralen). Dort wird statt

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}$

oft

${\displaystyle \int _{a}^{b}\mathrm {d} xf(x)}$

geschrieben, manchmal werden an verschiedenen Stellen sogar beide Schreibweisen benutzt.

Die zweite Schreibweise hat den Nachteil, dass die zu integrierende Funktion ${\displaystyle f(x)}$ nicht mehr durch ${\displaystyle \textstyle \int _{a}^{b}}$ und ${\displaystyle \mathrm {d} x}$ eingeklammert wird. Zudem können Missverständnisse zum Beispiel beim Lebesgue-Integral auftreten. Die alternative Schreibweise hat jedoch auch einige Vorzüge:

• Der Ausdruck ${\displaystyle \textstyle \int _{a}^{b}\mathrm {d} x}$ hebt hervor, dass das Integral ein linearer Operator ist, der auf alles rechts von ihm wirkt.
• Oft tauchen in der Physik Integrale auf, bei denen die zu integrierende Funktion mehrere Zeilen lang ist, oder es wird über mehrere Unbekannte ${\displaystyle x_{1},x_{2},\dotsc ,x_{n}}$ integriert. Dann weiß man bei der Schreibweise ${\displaystyle \textstyle \int _{a}^{b}\mathrm {d} xf(x)}$ schon zu Beginn des Integrals, welche Variablen überhaupt und über welche Grenzen integriert werden. Ferner ist dann die Zuweisung von Variablen zu Grenzen einfacher.
• Die Kommutativität der Produkte bei den in der Riemann’schen Näherung auftretenden Summanden ${\displaystyle \Delta x_{n}\cdot f(x_{n})}$ wird betont.

Beispiel:

${\displaystyle \int _{a_{1}}^{a_{2}}\mathrm {d} t\int _{b_{1}}^{b_{2}}\mathrm {d} x_{1}\int _{c_{1}}^{c_{2}}\mathrm {d} x_{2}\int _{d_{1}}^{d_{2}}\mathrm {d} x_{3}\,f(x_{1},x_{2},x_{3},t)}$

statt

${\displaystyle \int _{a_{1}}^{a_{2}}\int _{b_{1}}^{b_{2}}\int _{c_{1}}^{c_{2}}\int _{d_{1}}^{d_{2}}f(x_{1},x_{2},x_{3},t)\,\mathrm {d} x_{3}\mathrm {d} x_{2}\mathrm {d} x_{1}\mathrm {d} t}$

• Ist ${\displaystyle f(x)\leq g(x)}$ für alle ${\displaystyle a\leq x\leq b}$, so ist

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x\leq \int _{a}^{b}g(x)\,\mathrm {d} x.}$

• Bezeichnet man mit ${\displaystyle \|f\|_{\infty }}$ die Supremumsnorm von ${\displaystyle f}$ auf ${\displaystyle [a,b]}$, so gilt

${\displaystyle \left|\int _{a}^{b}f(x)\,\mathrm {d} x\right|\leq (b-a)\cdot \|f\|_{\infty }.}$

• Ist ${\displaystyle |f(x)-g(x)|<\varepsilon }$ für alle ${\displaystyle a\leq x\leq b}$ mit einer festen Zahl ${\displaystyle \varepsilon >0}$, so gilt

${\displaystyle \left|\int _{a}^{b}f(x)\,\mathrm {d} x-\int _{a}^{b}g(x)\,\mathrm {d} x\right|\leq (b-a)\cdot \varepsilon .}$

Daraus folgt: Ist ${\displaystyle (f_{n})_{n\in \mathbb {N} }}$ eine Folge von integrierbaren Funktionen, die gleichmäßig gegen eine (integrierbare) Funktion ${\displaystyle f}$ konvergiert, so ist

${\displaystyle \lim _{n\to \infty }\int _{a}^{b}f_{n}(x)\,\mathrm {d} x=\int _{a}^{b}f(x)\,\mathrm {d} x.}$

Mit anderen Worten: Das Integral ist ein stetiges Funktional für die Supremumsnorm.

• Integrale von Treppenfunktionen: Ist ${\displaystyle f}$ eine Treppenfunktion, das heißt, ist ${\displaystyle [a,b]}$ eine disjunkte Vereinigung von Intervallen ${\displaystyle I_{k}}$ der Längen ${\displaystyle L_{k}}$, sodass ${\displaystyle f}$ auf ${\displaystyle I_{k}}$ konstant mit Wert ${\displaystyle c_{k}}$ ist, so gilt:

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=\sum _{k=1}^{n}L_{k}\cdot c_{k}.}$

Das Integral ist somit gleich der Summe der orientierten Flächeninhalte der Rechtecke zwischen dem Funktionsgraphen von ${\displaystyle f}$ und der ${\displaystyle x}$-Achse.

Die Integration ist eine nicht-eindeutige Umkehrung der Differentiation. Um dies zu präzisieren, wird der Begriff der Stammfunktion benötigt: Ist ${\displaystyle f}$ eine Funktion, so heißt eine Funktion ${\displaystyle F}$ eine Stammfunktion von ${\displaystyle f}$, wenn die Ableitung von ${\displaystyle F}$ gleich ${\displaystyle f}$ ist:

${\displaystyle F'=f}$

Nicht-eindeutig ist diese Umkehrung, weil verschiedene Funktionen, die sich nur um einen konstanten Summanden unterscheiden, ein und dieselbe Ableitung haben. Daraus folgt, dass eine Funktion, zu der es eine Stammfunktion gibt, dann gleich unendlich viele Stammfunktionen hat.

Der Hauptsatz der Differential- und Integralrechnung stellt eine Beziehung zwischen Stammfunktionen und Integralen her. Er besagt: Ist ${\displaystyle f}$ eine stetige Funktion auf einem Intervall ${\displaystyle [a,b]}$ und ist ${\displaystyle F}$ eine Stammfunktion von ${\displaystyle f}$, so gilt

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=F(b)-F(a).}$

Die rechte Seite wird oft abkürzend als

${\displaystyle {\Big [}F(x){\Big ]}_{a}^{b}={\Big [}F(x){\Big ]}_{x=a}^{x=b}=F(x){\Big |}_{a}^{b}=F(x){\Big |}_{x=a}^{x=b}}$ oder Ähnliches

geschrieben.

Dieser Zusammenhang ist die hauptsächliche Methode zur expliziten Auswertung von Integralen. Die Schwierigkeit liegt meist im Auffinden einer Stammfunktion.

Die bloße Existenz ist theoretisch gesichert: Die Integralfunktion

${\displaystyle x\mapsto F_{a}(x):=\int _{a}^{x}f(t)\,\mathrm {d} t}$

ist für jedes ${\displaystyle a}$ eine Stammfunktion von ${\displaystyle f}$.

Man kann zu einer Stammfunktion eine Konstante addieren und erhält wieder eine Stammfunktion: Ist ${\displaystyle F}$ eine Stammfunktion zu einer Funktion ${\displaystyle f}$ und ist ${\displaystyle c\in \mathbb {R} }$ eine Konstante, so ist

${\displaystyle (F+c)'=F\!\,'+0=F'=f.}$

Zwei Stammfunktionen derselben auf einem Intervall definierten Funktion unterscheiden sich um eine Konstante: Sind ${\displaystyle F}$ und ${\displaystyle G}$ Stammfunktionen einer Funktion ${\displaystyle f}$, so ist

${\displaystyle (F-G)\!\,'=F'-G'=f-f=0,}$

also ist die Differenz ${\displaystyle F-G}$ eine Konstante. Ist der Definitionsbereich von ${\displaystyle f}$ kein Intervall, so ist die Differenz zweier Stammfunktionen lediglich lokal konstant.

Eine Stammfunktion wird auch als unbestimmtes Integral von ${\displaystyle f(x)}$ bezeichnet – manchmal ist damit aber auch die Menge aller Stammfunktionen gemeint. Ist ${\displaystyle F(x)}$ eine Stammfunktion, so schreibt man häufig unpräzise

${\displaystyle \int f(x)\,\mathrm {d} x=F(x)+C,}$

um anzudeuten, dass jede Stammfunktion von ${\displaystyle f}$ die Form ${\displaystyle F(x)+C}$ mit einer Konstante ${\displaystyle C}$ hat. Die Konstante ${\displaystyle C}$ heißt Integrationskonstante.

Man beachte, dass die Schreibweise

${\displaystyle \int f(x)\,\mathrm {d} x}$

jedoch auch häufig in Formeln benutzt wird, um anzudeuten, dass Gleichungen für beliebige, konsistent gewählte Grenzen gelten; beispielsweise ist mit

${\displaystyle \int cf(x)\,\mathrm {d} x=c\int f(x)\,\mathrm {d} x}$

gemeint, dass

${\displaystyle \int _{a}^{b}cf(x)\,\mathrm {d} x=c\int _{a}^{b}f(x)\,\mathrm {d} x}$

für beliebige ${\displaystyle a,b}$ gilt.

Siehe dazu den Artikel: Tabelle von Ableitungs- und Stammfunktionen oder unbestimmte Integrale in der Formelsammlung Mathematik.

Im Gegensatz zur Ableitungsfunktion ist die explizite Berechnung einer Stammfunktion bei vielen Funktionen sehr schwierig oder nicht möglich. Oft schlägt man Integrale deshalb in Tabellenwerken (z. B. einer Integraltafel) nach. Zur manuellen Berechnung einer Stammfunktion ist häufig die geschickte Anwendung der folgenden Standardtechniken hilfreich.

Die partielle Integration ist die Umkehrung der Produktregel der Differentialrechnung. Sie lautet:

${\displaystyle \int f'(x)\cdot g(x)\,\mathrm {d} x=f(x)\cdot g(x)-\int f(x)\cdot g'(x)\,\mathrm {d} x}$

Diese Regel ist dann von Vorteil, wenn die Funktion ${\displaystyle f(x)\cdot g'(x)}$ einfacher als die Funktion ${\displaystyle f'(x)\cdot g(x)}$ zu integrieren ist. Hierbei sind jedoch die Produkte und nicht die Faktoren selbst zu bewerten.

Beispiel:

${\displaystyle \int x\ln(x)\,\mathrm {d} x}$

Setzt man

${\displaystyle f'(x)=x\,}$ und ${\displaystyle g(x)=\ln(x)\,}$

so ist

${\displaystyle f(x)={\frac {x^{2}}{2}}}$ und ${\displaystyle g'(x)={\frac {1}{x}}}$

und man erhält

${\displaystyle {\begin{aligned}\int x\ln(x)\,\mathrm {d} x&={\frac {x^{2}}{2}}\ln(x)-\int {\frac {x^{2}}{2}}\cdot {\frac {1}{x}}\,\mathrm {d} x\\&={\frac {x^{2}}{2}}\left(\ln(x)-{\frac {1}{2}}\right).\end{aligned}}}$

Die Substitutionsregel ist ein wichtiges Hilfsmittel, um einige schwierige Integrale zu berechnen, da sie bestimmte Änderungen der zu integrierenden Funktion bei gleichzeitiger Änderung der Integrationsgrenzen erlaubt. Sie ist das Gegenstück zur Kettenregel in der Differentialrechnung.

Sei ${\displaystyle \varphi (x)=f(g(x))\cdot g'(x)}$ mit ${\displaystyle g'\neq 0}$ und ${\displaystyle F}$ eine Stammfunktion von ${\displaystyle f}$, so ist ${\displaystyle \Phi (x)=F(g(x))}$ eine Stammfunktion von ${\displaystyle \varphi }$, denn es gilt

${\displaystyle {\frac {\varphi (x)}{g'(x)}}=f(g(x))}$

und mit der Substitution

${\displaystyle z=g(x),\quad \mathrm {d} z=g'(x)\mathrm {d} x}$

schließlich

${\displaystyle {\begin{aligned}\int _{a}^{b}f(g(x))g'(x)\mathrm {d} x&=\int _{g(a)}^{g(b)}f(z)\mathrm {d} z\\&=F(g(b))-F(g(a))\\&=\Phi (b)-\Phi (a).\end{aligned}}}$

Bei gebrochenrationalen Funktionen führt häufig eine Polynomdivision oder eine Partialbruchzerlegung zu einer Umformung der Funktion, die es erlaubt, eine der Integrationsregeln anzuwenden.

Oft ist es möglich, unter Ausnutzung der speziellen Form des Integranden die Stammfunktion zu bestimmen.

Eine weitere Möglichkeit besteht darin, bei einem bekannten Integral zu beginnen und dieses durch Integrationstechniken solange umzuformen, bis das gewünschte Integral entsteht. Beispiel:

Um ${\displaystyle \textstyle \int {\frac {\mathrm {d} x}{(1+x^{2})^{2}}}}$ zu bestimmen, wird ein bekanntes ähnliches Integral partiell integriert:

${\displaystyle {\begin{aligned}\arctan x&=\int 1\cdot {\frac {1}{1+x^{2}}}\,\mathrm {d} x\\&=x\cdot {\frac {1}{1+x^{2}}}+\int x\cdot {\frac {2x}{(1+x^{2})^{2}}}\,\mathrm {d} x\\&={\frac {x}{1+x^{2}}}+\int \left({\frac {2x^{2}}{(1+x^{2})^{2}}}+{\frac {2}{(1+x^{2})^{2}}}\right)\,\mathrm {d} x-\int {\frac {2}{(1+x^{2})^{2}}}\,\mathrm {d} x\\&={\frac {x}{1+x^{2}}}+2\int {\frac {1+x^{2}}{(1+x^{2})^{2}}}\,\mathrm {d} x-2\int {\frac {1}{(1+x^{2})^{2}}}\,\mathrm {d} x\\&={\frac {x}{1+x^{2}}}+2\arctan x-2\int {\frac {\mathrm {d} x}{(1+x^{2})^{2}}}\end{aligned}}}$

Durch Umstellen erhält man

${\displaystyle \int {\frac {\mathrm {d} x}{(1+x^{2})^{2}}}={\frac {1}{2}}\left({\frac {x}{1+x^{2}}}+\arctan x\right).}$

Soll eine Funktion ${\displaystyle f}$ mehrfach integriert werden, liefert die Cauchy-Formel für mehrfache Integration für das ${\displaystyle n}$-te iterierte Integral von ${\displaystyle f}$ am Punkt ${\displaystyle x}$

${\displaystyle I^{n}(x)=\int _{a}^{x}\int _{a}^{\sigma _{1}}\cdots \int _{a}^{\sigma _{n-1}}f(\sigma _{n})\,\mathrm {d} \sigma _{n}\cdots \,\mathrm {d} \sigma _{2}\,\mathrm {d} \sigma _{1}}$

das Integral

${\displaystyle I^{n}(x)={\frac {1}{(n-1)!}}\int _{a}^{x}\left(x-t\right)^{n-1}f(t)\,\mathrm {d} t}$.

Es soll der „mittlere Wert“ ${\displaystyle m}$ ermittelt werden, den eine auf einem Intervall definierte Funktion ${\displaystyle f}$ annimmt. Da ${\displaystyle f}$ im Allgemeinen unendlich viele verschiedene Werte annimmt, wird man diesen mittleren Wert dadurch annähern, dass man ${\displaystyle f}$ zunächst nur an endlich vielen Stellen ${\displaystyle \{x_{1},x_{2},\dots ,x_{n}\}}$ auswertet, die gleichmäßig über ${\displaystyle [a,b]}$ verteilt sind, und dann das arithmetische Mittel

${\displaystyle {\frac {f(x_{1})+\cdots +f(x_{n})}{n}}}$

bildet. Mit ${\displaystyle \Delta x=(b-a)/n}$ erhält man somit als Annäherung für den mittleren Wert von ${\displaystyle f}$

${\displaystyle m\approx {\frac {1}{b-a}}\sum _{k=1}^{n}f(x_{k})\Delta x}$.

Die Approximation wird umso genauer, je größer die Anzahl der Stellen ${\displaystyle n}$ ist, die in diese Summe einfließen. Für ${\displaystyle n\rightarrow \infty }$ erhält man schließlich als genaue Formel für den Mittelwert der Funktion

${\displaystyle m=\lim _{n\to \infty }\left({\frac {1}{b-a}}\sum _{k=1}^{n}f(x_{k})\Delta x\right).}$

Existiert der Grenzwert auf der rechten Seite, so handelt es sich um das Integral der Funktion über ${\displaystyle [a,b].}$ Deshalb ist der Mittelwert einer Funktion definiert als

${\displaystyle m={\frac {1}{b-a}}\int _{a}^{b}f(x)\,\mathrm {d} x.}$

Diese Definition stimmt für Treppenfunktionen mit dem üblichen Mittelwertbegriff übereinstimmt und ist somit eine Verallgemeinerung der arithmetischen Mittels.

Ein physikalisches Phänomen, an dem der Integralbegriff erklärt werden kann, ist der freie Fall eines Körpers im Schwerefeld der Erde. Die Geschwindigkeit ${\displaystyle v}$ eines Körpers zur Zeit ${\displaystyle t}$ wird durch die Formel

${\displaystyle v=g\cdot t}$

beschrieben. Dabei ist ${\displaystyle g}$ die konstante Erdbeschleunigung, die in Mitteleuropa ca. 9,81 m/s² beträgt.

Nun soll aber die Wegstrecke ${\displaystyle l}$ berechnet werden, die der fallende Körper bis zu einer bestimmten Zeit ${\displaystyle T}$ zurücklegt. Die Formel ${\displaystyle l=v\cdot T}$ („Weg = Geschwindigkeit × Zeit“) ist nur bei einer konstanten Geschwindigkeit gültig. Unter dem Einfluss der Erdbeschleunigung nimmt die Geschwindigkeit ${\displaystyle v}$ des Körpers jedoch stetig mit der Zeit zu. Um das Problem zu lösen, zerlegt man den gesamten Zeitraum in sehr kurze Zeitintervalle ${\displaystyle \Delta t}$; während jedes Zeitintervalls ändert sich die Geschwindigkeit nur wenig, so dass die Formel „Weg = Geschwindigkeit × Zeit“ zumindest näherungsweise gilt. Die innerhalb eines kurzen Zeitraums ${\displaystyle \Delta t}$ zurückgelegte Teilstrecke ${\displaystyle \Delta l}$ beträgt daher

${\displaystyle \Delta l\approx g\cdot t\,\cdot \Delta t}$.

Die gesamte Wegstrecke erhält man näherungsweise als Summe aller Teilstrecken:

${\displaystyle l\approx \sum g\cdot t\,\cdot \Delta t.}$

Wenn man nun die Zeitdifferenzen ${\displaystyle \Delta t}$ gegen Null streben lässt, verschwinden die Approximationsfehler und man erhält die exakte Wegstrecke als

${\displaystyle l=\lim _{\Delta t\to 0}\sum g\cdot t\,\cdot \Delta t.}$

Die rechte Seite der Gleichung ist gerade das Integral über ${\displaystyle g\cdot t}$. Also ist die Wegstrecke das Integral der Geschwindigkeit über die Zeit:

${\displaystyle l=\int _{0}^{T}g\cdot t\;\mathrm {d} t.}$

Das Integral lässt sich z. B. mit dem Hauptsatz der Analysis auswerten:

${\displaystyle l=\,{\frac {g}{2}}\cdot T^{2}.}$

Die allgemeine Lösung führt zur Bewegungsgleichung des im konstanten Schwerefeld fallenden Körpers:

${\displaystyle l={\frac {g}{2}}\cdot t^{2}.}$

Weitere Beispiele sind:

• Die Energie ist das Integral der Leistung über die Zeit.
• Die elektrische Ladung eines Kondensators ist das Integral des durch ihn fließenden Stromes über die Zeit.
• Das Integral des Produktes der spektralen Bestrahlungsstärke (E_e(ν) in W/m²Hz) mit der spektralen Hellempfindlichkeitskurve des Auges liefert die Beleuchtungsstärke (E in Lux = Lumen/m²).
• Das Integral der Strömungsgeschwindigkeit (Längskomponente) über den Querschnitt eines Rohres liefert den gesamten Volumenstrom durch das Rohr (weitere mehrdimensionale Integrale siehe unten).

Eine Regelfunktion ist eine Funktion, die sich gleichmäßig durch Treppenfunktionen approximieren lässt. Aufgrund der erwähnten Kompatibilität des Integrals mit gleichmäßigen Limites kann man für eine Regelfunktion ${\displaystyle f}$, die gleichmäßiger Limes einer Folge ${\displaystyle t_{n}}$ von Treppenfunktionen ist, das Integral definieren als

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=\lim _{n\to \infty }\int _{a}^{b}t_{n}(x)\,\mathrm {d} x,}$

wobei das Integral für Treppenfunktionen durch die oben angegebene Formel definiert wird.

Die Klasse der Regelfunktionen umfasst alle stetigen Funktionen und alle monotonen Funktionen, ebenso alle Funktionen ${\displaystyle f}$, für die sich ${\displaystyle [a,b]}$ in endlich viele Intervalle ${\displaystyle I_{k}}$ unterteilen lässt, sodass die Einschränkung von ${\displaystyle f}$ auf ${\displaystyle I_{k}}$ eine stetige oder monotone Funktion auf dem abgeschlossenen Intervall ${\displaystyle {\bar {I}}_{k}}$ ist, d. h. alle stückweise stetigen Funktionen. Sie umfasst außerdem Funktionen von beschränkter Variation, da sich so eine Funktion als Differenz zweier monoton steigender Funktionen darstellen lässt. Für viele praktische Zwecke ist diese Integralkonstruktion völlig ausreichend.

Es gibt auch stetige Funktionen mit unendlicher Variation wie z. B. die durch ${\displaystyle 0\mapsto 0}$ und ${\displaystyle t\mapsto t\cos {\tfrac {\pi /2}{t}}}$ für ${\displaystyle 0<t\leq 1}$ auf dem Intervall ${\displaystyle [0,\ 1]}$ definierte Funktion (siehe Variation).

Ein Ansatz zur Berechnung des Integrals nach Riemann ist die Approximation der zu integrierenden Funktion durch eine Treppenfunktion; allerdings nicht durch gleichmäßige Approximation der Funktion selbst, sondern durch Approximation des Flächeninhalts durch Rechtecksummen.

Die Fläche wird durch die Summe der Flächeninhalte der einzelnen Rechtecke unter den einzelnen „Treppenstufen“ angenähert. Zu jeder Zerlegung des Integrationsintervalls kann man dazu einen beliebigen Funktionswert innerhalb jedes Teilintervalls als Höhe der Stufe wählen.

Dies sind die nach dem deutschen Mathematiker Bernhard Riemann bezeichneten Riemann-Summen. Wählt man in jedem Teilintervall der Zerlegung gerade das Supremum der Funktion als Höhe des Rechtecks, so ergibt sich die Obersumme, mit dem Infimum die Untersumme.

Das Riemannsche Integral lässt sich mit Hilfe von Ober- und Untersummen definieren, siehe Riemannsches Integral. Konvergieren Ober- und Untersummen gegen den gleichen Grenzwert, so ist dieser Grenzwert das Integral im Sinne von Riemann. Integrierbar in diesem Sinne sind z. B. sämtliche Funktionen, für die das Cauchy-Integral existiert.

Das Riemann-Integral existiert z. B. nicht für die Indikatorfunktion der rationalen Zahlen im Intervall ${\displaystyle [0,\ 1]}$, d. h. für die Dirichlet-Funktion. Deshalb wurden erweiterte Integralbegriffe von Henri Léon Lebesgue (Lebesgue-Integral), Thomas Jean Stieltjes (Stieltjesintegral) und Alfréd Haar eingeführt, die für stetige Integranden das Riemann-Integral reproduzieren.

Beim Stieltjes-Integral geht man von monotonen Funktionen ${\displaystyle g}$ aus, oder von solchen mit endlicher Variation, das sind Differenzen von zwei monotonen Funktionen, und definiert für stetige Funktionen ${\displaystyle f}$ Riemann-Stieltjes’sche Summen als

${\displaystyle \sum _{i=0}^{n-1}\,f(x_{i})\,\left(g(x_{i+1})-g(x_{i})\right).}$

Durch Limesbildung in der üblichen Weise erhält man dann das sogenannte Riemann-Stieltjes-Integral ${\displaystyle \textstyle \int _{I}\,f\,\mathrm {d} g}$.

Solche Integrale sind auch dann definiert, wenn die Funktion ${\displaystyle g}$ nicht differenzierbar ist (andernfalls gilt ${\displaystyle \mathrm {d} g(x)=g'(x)\,\mathrm {d} x}$). Ein bekanntes Gegenbeispiel ist die sogenannte Heaviside-Funktion ${\displaystyle \Theta }$, deren Wert gleich null für negative Argumente, eins für positive Argumente und z. B. ${\displaystyle \textstyle {\frac {1}{2}}}$ an der Stelle ${\displaystyle 0}$ ist. Man schreibt, für ${\displaystyle g=\Theta }$, ${\displaystyle \mathrm {d} g(x)=\delta (x)\mathrm {d} x}$ und erhält so die „verallgemeinerte Funktion“ ${\displaystyle \delta }$, das sogenannte Diracmaß, als ein nur im Punkt ${\displaystyle 0}$ definiertes Maß.

Einen moderneren und – in vielerlei Hinsicht – besseren Integralbegriff als den des Riemann’schen Integrals liefert das Lebesgue-Integral. Es erlaubt zum Beispiel die Integration über allgemeine Maßräume. Das bedeutet, dass man Mengen ein Maß zuordnen kann, das nicht notwendig mit ihrer geometrischen Länge bzw. ihrem Rauminhalt übereinstimmen muss, so zum Beispiel Wahrscheinlichkeitsmaße in der Wahrscheinlichkeitstheorie. Das Maß, das dem intuitiven Längen- bzw. Volumenbegriff entspricht, ist das Lebesgue-Maß. In der Regel wird das Integral über dieses Maß als Lebesgue-Integral bezeichnet. Für jede Funktion, die über einem kompakten Intervall Riemann-integrierbar ist, existiert auch das entsprechende Lebesgue-Integral und die Werte beider Integrale stimmen überein. Umgekehrt sind aber nicht alle Lebesgue-integrierbaren Funktionen auch Riemann-integrierbar. Das bekannteste Beispiel dafür ist die Dirichlet-Funktion, also die Funktion, die für rationale Zahlen den Wert Eins, aber für irrationale Zahlen den Wert Null hat. Neben der größeren Klasse an integrierbaren Funktionen zeichnet sich das Lebesgue-Integral gegenüber dem Riemann-Integral vor allem durch die besseren Konvergenzsätze aus (Satz von der monotonen Konvergenz, Satz von der majorisierten Konvergenz) und die besseren Eigenschaften der durch das Lebesgue-Integral normierten Funktionenräume (etwa Vollständigkeit).

In der modernen Mathematik versteht man unter Integral oder Integrationstheorie häufig den lebesgueschen Integralbegriff.

Das Riemann-Integral ist (im eindimensionalen Raum) nur für kompakte, also beschränkte und abgeschlossene, Intervalle definiert. Eine Verallgemeinerung auf unbeschränkte Definitionsbereiche oder Funktionen mit Singularitäten bietet das uneigentliche Integral. Auch in der Lebesgue-Theorie können uneigentliche Integrale betrachtet werden, jedoch ist dies nicht so ergiebig, da man mit dem Lebesgue-Integral schon viele Funktionen mit Singularitäten oder unbeschränktem Definitionsbereich integrieren kann.

Oft ist es schwierig oder nicht möglich, eine Stammfunktion explizit anzugeben. Allerdings reicht es in vielen Fällen auch aus, das bestimmte Integral näherungsweise zu berechnen. Man spricht dann von numerischer Quadratur oder numerischer Integration. Viele Verfahren zur numerischen Quadratur bauen auf einer Approximation der Funktion durch einfacher integrierbare Funktionen auf, zum Beispiel durch Polynome. Die Trapezregel oder auch die simpsonsche Formel (deren Spezialfall als keplersche Fassregel bekannt ist) sind Beispiele dafür, hier wird durch die Funktion ein Interpolationspolynom gelegt und dann integriert.

Bereits lange vor der Verbreitung von Computern wurden für die numerische Integration Verfahren zur automatischen Schrittweitensteuerung entwickelt. Heute bietet die Computeralgebra die Möglichkeit, komplexe Integrale numerisch in immer kürzeren Zeiten bzw. immer genauer zu lösen, wobei auch bei leistungsfähigen Systemen noch Schwierigkeiten bei uneigentlichen Integralen bestehen, für deren Berechnung oft spezielle Verfahren wie Gauß-Kronrod angewendet werden müssen. Ein Beispiel für ein solches hartes Integral ist:

${\displaystyle \int _{0}^{\infty }{\frac {\ln(1+x)}{\ln ^{2}x+\pi ^{2}}}\cdot {\frac {\mathrm {d} x}{x^{2}}}=\gamma }$

Klassische Verfahren sind z. B. die Eulersche Summenformel, bei der das bestimmte Integral durch eine im Allgemeinen asymptotische Reihe approximiert wird. Weitere Methoden basieren auf der Theorie der Differenzenrechnung, als wichtiges Beispiel ist hier die Gregorysche Integrationsformel zu nennen.

Es gibt eine Reihe von Verfahren, mit denen bestimmte und uneigentliche Integrale exakt in symbolischer Form berechnet werden können.

Falls ${\displaystyle f}$ stetig und zu ${\displaystyle f}$ eine Stammfunktion ${\displaystyle F}$ bekannt ist, lässt sich das bestimmte Integral

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=F(b)-F(a)}$

durch den Hauptsatz berechnen. Problematisch ist, dass die Operation des unbestimmten Integrierens zu einer Erweiterung vorgegebener Funktionsklassen führt. Z. B. ist das Integrieren innerhalb der Klasse der rationalen Funktionen nicht abgeschlossen und führt auf die Funktionen ${\displaystyle \ln }$ und ${\displaystyle \arctan }$. Auch die Klasse der so genannten elementaren Funktionen ist nicht abgeschlossen. So hat Joseph Liouville bewiesen, dass die Funktion ${\displaystyle e^{-x^{2}}}$ keine elementare Stammfunktion besitzt. Leonhard Euler war einer der ersten, die Methoden zur exakten Berechnung bestimmter und uneigentlicher Integrale ohne Bestimmung einer Stammfunktion entwickelten. Im Laufe der Zeit sind zahlreiche allgemeinere und speziellere Methoden zur bestimmten Integration entstanden:

• Benutzung des Residuensatzes
• Darstellung des von einem Parameter abhängigen Integrals durch spezielle Funktionen
• Differentiation oder Integration des Integrals nach einem Parameter und Vertauschung der Grenzprozesse
• Benutzung einer Reihenentwicklung des Integranden mit gliedweiser Integration
• durch partielle Integration und Substitution das Integral auf sich selbst oder ein anderes zurückführen

Bis zum Ende des 20. Jahrhunderts sind zahlreiche (teils mehrbändige) Integraltafeln mit bestimmten Integralen entstanden. Zur Illustration der Problematik einige Beispiele:

${\displaystyle \int _{0}^{1}{\frac {\ln(1+x)}{x^{2}+1}}\,\mathrm {d} x={\frac {\pi }{8}}\ln 2}$

${\displaystyle \int _{0}^{\pi }\ln \sin x\,\mathrm {d} x=-\pi \ln 2}$

Es gibt eine Reihe von bestimmten und uneigentlichen Integralen, die eine gewisse Bedeutung für die Mathematik haben und daher einen eigenen Namen tragen:

• Eulersche Integrale erster und zweiter Art
• Gaußsches Fehlerintegral

${\displaystyle \int _{-\infty }^{\infty }e^{-t^{2}}\,\mathrm {d} t={\sqrt {\pi }}}$

• Fresnel-Integrale

${\displaystyle \int _{0}^{\infty }\cos t^{2}\,\mathrm {d} t=\int _{0}^{\infty }\sin t^{2}\,\mathrm {d} t={\tfrac {1}{4}}{\sqrt {2\pi }}}$

• Raabesches Integral

${\displaystyle \int \limits _{a}^{a+1}\log \Gamma (t)\,\mathrm {d} t={\tfrac {1}{2}}\log 2\pi +a\log a-a,\quad a\geq 0,}$    und speziell für ${\displaystyle a=0}$ und ${\displaystyle a=e}$: ${\displaystyle \int _{0}^{1}\log \Gamma (t)\,\mathrm {d} t={\tfrac {1}{2}}\log 2\pi }$

• Frullanische Integrale

${\displaystyle \int _{0}^{\infty }{\frac {f(ax)-f(bx)}{x}}\,\mathrm {d} x}$

Ist ${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$ ein Weg, also eine stetige Abbildung, und ${\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} }$ eine skalare Funktion, so ist das Wegintegral von ${\displaystyle f}$ entlang ${\displaystyle \gamma }$ definiert als

${\displaystyle \int _{\gamma }f(x)\,\mathrm {d} x=\int _{a}^{b}f(\gamma (t))\,\|{\dot {\gamma }}(t)\|\,\mathrm {d} t.}$

Ist ${\displaystyle f\equiv 1}$, so erhalten wir aus der obigen Formel die Länge der Kurve ${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{2}}$ (physikalisch gesprochen) als das Integral der Geschwindigkeit über die Zeit:

${\displaystyle L(\gamma )=\int _{a}^{b}\|{\dot {\gamma }}(t)\|\,\mathrm {d} t=\int _{a}^{b}{\sqrt {{\dot {x}}(t)^{2}+{\dot {y}}(t)^{2}}}\,\mathrm {d} t}$

In der Physik werden häufig Wegintegrale der folgenden Form verwendet: ${\displaystyle {\vec {f}}}$ ist eine Vektorfunktion ${\displaystyle \mathbb {R} ^{n}\to \mathbb {R} ^{n}}$, und es wird das Integral

${\displaystyle \int _{\gamma }{\vec {f}}(x)\cdot \mathrm {d} x=\int _{a}^{b}\langle {\vec {f}}(\gamma (t)),{\dot {\gamma }}(t)\rangle \,\mathrm {d} t}$

betrachtet, wobei der Ausdruck in den gewinkelten Klammern ein Skalarprodukt darstellt.

In der Funktionentheorie, also der Erweiterung der Analysis auf Funktionen einer komplexen Veränderlichen, genügt es nicht mehr, untere und obere Integrationsgrenzen anzugeben. Zwei Punkte der komplexen Ebene können, anders als zwei Punkte auf der Zahlengeraden, durch viele Wege miteinander verbunden werden. Deshalb ist das bestimmte Integral in der Funktionentheorie grundsätzlich ein Wegintegral. Für geschlossene Wege gilt der Residuensatz, ein wichtiges Resultat von Cauchy: Das Integral einer meromorphen Funktion entlang eines geschlossenen Weges hängt allein von der Anzahl der umschlossenen Singularitäten ab. Es ist Null, falls sich im Integrationsgebiet keine Singularitäten befinden.

Als Beispiel wird das Volumen unter dem Graphen der Funktion ${\displaystyle f\colon \mathbb {R} ^{2}\to \mathbb {R} }$ mit ${\displaystyle f(x,y):=x^{2}+y}$ über dem Einheitsquadrat ${\displaystyle I:=[0,1]\times [0,1]}$ berechnet. Dazu teilt man das Integral über ${\displaystyle I}$ auf zwei Integrale auf, eines für die ${\displaystyle x}$- und eines für die ${\displaystyle y}$-Koordinate:

${\displaystyle {\begin{aligned}\int _{[0,\ 1]\times [0,\ 1]}f(x,y)\,\mathrm {d} (x,y)&=\int _{0}^{1}\int _{0}^{1}f(x,y)\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}\int _{0}^{1}(x^{2}+y)\,\mathrm {d} x\,\mathrm {d} y\\&=\int _{0}^{1}\left[{\tfrac {1}{3}}x^{3}+yx\right]_{x=0}^{1}\,\mathrm {d} y=\int _{0}^{1}\left({\tfrac {1}{3}}+y\right)\mathrm {d} y=\left[{\tfrac {1}{3}}y+{\tfrac {1}{2}}y^{2}\right]_{y=0}^{1}={\tfrac {5}{6}}\end{aligned}}}$

Für ${\displaystyle f\equiv 1}$ ergibt das Oberflächenintegral den Flächeninhalt der Integrationsfläche.

Für ${\displaystyle f\equiv 1}$ berechnet das Volumenintegral den Volumeninhalt des Integrationsbereiches.

Den Integralbegriff kann man auf den Fall verallgemeinern, dass die Trägermenge, auf der der Integrand ${\displaystyle f}$ operiert, nicht die Zahlengerade ${\displaystyle \mathbb {R} }$, sondern der ${\displaystyle n}$-dimensionale euklidische Raum ${\displaystyle \mathbb {R} ^{n}}$ ist.

Für mehrdimensionale Integrale, also auch Flächen- und Volumenintegrale, findet der Satz von Fubini Anwendung, der es erlaubt, die Integrale in beliebiger Reihenfolge über die einzelnen Koordinaten aufzuspalten und sie nacheinander abzuarbeiten:

${\displaystyle {\begin{aligned}\int _{V}f\left({\vec {r}}\right)\mathrm {d} ^{3}r&=\iiint f(x,y,z)\mathrm {d} z\,\mathrm {d} y\,\mathrm {d} x\\&=\int \left(\int \left(\int f(x,y,z)\mathrm {d} z\right)\mathrm {d} y\right)\mathrm {d} x\end{aligned}}}$

Die Integrationsgrenzen der eindimensionalen Integrale in ${\displaystyle x}$, ${\displaystyle y}$ und ${\displaystyle z}$ muss man aus der Begrenzung des Volumens ${\displaystyle V}$ ermitteln. Analog zu den uneigentlichen Integralen im Eindimensionalen (siehe oben) kann man aber auch Integrale über den gesamten, unbeschränkten ${\displaystyle n}$-dimensionalen Raum betrachten.

Die Verallgemeinerung der Substitutionsregel im Mehrdimensionalen ist der Transformationssatz. Sei ${\displaystyle \Omega \subset \mathbb {R} ^{d}}$ offen und ${\displaystyle \Phi \colon \Omega \to \mathbb {R} ^{d}}$ eine injektive, stetig differenzierbare Abbildung, für deren Funktionaldeterminante ${\displaystyle \det(D\Phi (x))\neq 0}$ für alle ${\displaystyle x\in \Omega }$ gilt. Dann ist

${\displaystyle \int _{\Phi (\Omega )}f(y)\,\mathrm {d} y=\int _{\Omega }f(\Phi (x))\left|\det(D\Phi (x))\right|\mathrm {d} x.}$

Insbesondere in vielen physikalischen Anwendungen ist die Integration über die Oberfläche eines Gebiets interessant. Solche Oberflächen werden üblicherweise durch Mannigfaltigkeiten beschrieben. Diese werden durch sogenannte Karten beschrieben.

Sei ${\displaystyle M}$ eine ${\displaystyle d}$-dimensionale Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ und ${\displaystyle U}$ ein Kartengebiet in ${\displaystyle M}$, also eine offene Teilmenge in ${\displaystyle M}$, für die es eine Karte gibt, die sie diffeomorph auf eine offene Teilmenge des ${\displaystyle \mathbb {R} ^{d}}$ abbildet. Ferner sei ${\displaystyle \gamma \colon \Omega \to U}$ eine Parametrisierung von ${\displaystyle U}$, also eine stetig differenzierbare Abbildung, deren Ableitung vollen Rang hat, die ${\displaystyle \Omega }$ homöomorph auf ${\displaystyle \gamma (\Omega )}$ abbildet. Dann ist das Integral einer Funktion auf dem Kartengebiet ${\displaystyle U}$ folgendermaßen definiert:

${\displaystyle \int _{U}f\mathrm {d} s:=\int _{\Omega }f(\gamma (u)){\sqrt {g^{\gamma }(u)}}\mathrm {d} u,}$

wobei ${\displaystyle g^{\gamma }(u)=\det((\gamma '(u))^{\mathsf {T}}\cdot \gamma '(u))}$ die Gramsche Determinante ist. Das rechte Integral kann mit den oben beschriebenen Methoden der mehrdimensionalen Integration ausgerechnet werden. Die Gleichheit folgt im Wesentlichen aus dem Transformationssatz.

Ist eine Zerlegung der 1 gegeben, die mit den Karten der Untermannigfaltigkeit verträglich ist, kann einfach getrennt über die Kartengebiete integriert und aufsummiert werden.

Für spezielle Funktionen lassen sich die Integrale über Untermannigfaltigkeiten einfacher ausrechnen. In der Physik besonders wichtig sind hierbei zwei Aussagen:

Zum einen der gaußsche Integralsatz, nach dem das Volumenintegral über die Divergenz eines Vektorfeldes gleich dem Oberflächenintegral über das Vektorfeld (dem Fluss des Feldes durch die Oberfläche) ist: Sei ${\displaystyle V\subset \mathbb {R} ^{n}}$ kompakt mit abschnittsweise glattem Rand ${\displaystyle \partial V}$. Der Rand sei orientiert durch ein äußeres Normalen-Einheitsfeld ${\displaystyle {\vec {n}}}$. Sei ferner ${\displaystyle {\vec {F}}}$ ein stetig differenzierbares Vektorfeld auf einer offenen Umgebung von ${\displaystyle V}$. Dann gilt

${\displaystyle \int _{V}\operatorname {div} {\vec {F}}\,\mathrm {d} ^{(n)}V=\oint _{\partial V}{\vec {F}}\cdot \mathrm {d} ^{(n-1)}{\vec {S}}}$

mit der Abkürzung ${\displaystyle \mathrm {d} ^{(n-1)}{\vec {S}}={\vec {n}}\,\mathrm {d} ^{(n-1)}S}$.

Durch diesen Satz wird die Divergenz als sogenannte Quellendichte des Vektorfeldes interpretiert. Durch die Indizes ${\displaystyle (n)}$ bzw. ${\displaystyle (n-1)}$ am ${\displaystyle \mathrm {d} }$-Operator wird die Dimension der jeweiligen Integrationsmannigfaltigkeit zusätzlich betont.

Bei expliziter Verwendung von Mehrfachintegralen wird (unter Verzicht auf die Indizierung) für ${\displaystyle n=3}$:

${\displaystyle \iiint _{V}\operatorname {div} \,{\vec {F}}({\vec {x}})\,\mathrm {d} V=\iint _{\partial V}{\vec {F}}\cdot \mathrm {d} {\vec {S}}}$

Es folgt: Das Integral der Divergenz über das gesamte Volumen ist gleich dem Integral des Flusses aus der Oberfläche.

Zum zweiten der Satz von Stokes, der eine Aussage der Differentialgeometrie ist und sich im Spezialfall des dreidimensionalen Raums direkt mit Mehrfachintegralen schreiben lässt.

Ist ${\displaystyle M}$ eine zweidimensionale Untermannigfaltigkeit des dreidimensionalen euklidischen Raumes ${\displaystyle \mathbb {R} ^{3}}$, so gilt

${\displaystyle \iint _{M}\operatorname {rot} {\vec {F}}\cdot \mathrm {d} {\vec {S}}=\int _{\partial M}{\vec {F}}\cdot \mathrm {d} {\vec {r}},}$

wobei ${\displaystyle \operatorname {rot} {\vec {F}}}$ die Rotation des Vektorfeldes ${\displaystyle {\vec {F}}}$ bezeichnet.

Durch diesen Satz wird die Rotation eines Vektorfeldes als sogenannte Wirbeldichte des Vektorfeldes interpretiert; dabei ist ${\displaystyle \mathrm {d} {\vec {r}}}$ der dreikomponentige Vektor ${\displaystyle (\mathrm {d} x,\mathrm {d} y,\mathrm {d} z)}$ und der Rand ${\displaystyle \partial M}$ von ${\displaystyle M}$ eine geschlossene Kurve im ${\displaystyle \mathbb {R} ^{3}}$.

Die Integration von Funktionen, die nicht reell- oder komplexwertig sind, sondern Werte in einem allgemeineren Vektorraum annehmen, ist ebenfalls auf verschiedenste Arten möglich.

Die direkte Verallgemeinerung des Lebesgue-Integrals auf Banachraum-wertige Funktionen ist das Bochner-Integral. Viele Ergebnisse der eindimensionalen Theorie übertragen sich dabei wortwörtlich auf Banachräume.

Auch die Definition des Riemann-Integrals mittels Riemann’scher Summen auf vektorwertige Funktionen ${\displaystyle f\colon [a,b]\to V}$ zu übertragen, fällt nicht schwer. Ein entscheidender Unterschied ist hierbei jedoch, dass dann nicht mehr jede Riemann-integrierbare Funktion Bochner-integrierbar ist.

Eine gemeinsame Verallgemeinerung des Bochner- und Riemann-Integrals, die diesen Mangel behebt, ist das McShane-Integral, das sich am einfachsten über verallgemeinerte Riemann’sche Summen definieren lässt.

Auch das Birkhoff-Integral ist eine gemeinsame Verallgemeinerung des Bochner- und Riemann-Integrals. Im Gegensatz zum McShane-Integral benötigt die Definition des Birkhoff-Integrals jedoch keine topologische Struktur im Definitionsbereich der Funktionen. Sind jedoch die Voraussetzungen für die McShane-Integration erfüllt, so ist jede Birkhoff-integrierbare Funktion auch McShane-integrierbar.^[1]

Außerdem ist noch das Pettis-Integral als nächster Verallgemeinerungsschritt erwähnenswert. Es nutzt eine funktionalanalytische Definition, bei der die Integrierbarkeit auf den eindimensionalen Fall zurückgeführt wird: Sei dafür ${\displaystyle (\Omega ,{\mathcal {A}},\mu )}$ ein Maßraum. Eine Funktion ${\displaystyle f\colon \Omega \to V}$ heißt dabei Pettis-integrierbar, wenn für jedes stetige Funktional ${\displaystyle \lambda \in V'}$ die Funktion ${\displaystyle \lambda \circ f\colon \Omega \to \mathbb {R} }$ Lebesgue-integrierbar ist und für jede messbare Menge ${\displaystyle A\in {\mathcal {A}}}$ ein Vektor ${\displaystyle x_{A}\in V}$ existiert, sodass

${\displaystyle \forall \lambda \in V'\colon \ \lambda (x_{A})=\int _{A}{\lambda \circ f}\,\mathrm {d} \mu }$

gilt. Der Vektor ${\displaystyle x_{A}}$ wird dann passenderweise mit ${\displaystyle \textstyle \int _{A}f\,\mathrm {d} \mu }$ bezeichnet.

Für Funktionen ${\displaystyle f\colon [a,b]\to V}$, die Werte in einem separablen Banachraum ${\displaystyle V}$ annehmen, stimmt das Pettis-Integral mit dem McShane- und dem Bochner-Integral überein. Wichtigster Spezialfall all dieser Definitionen ist der Fall von Funktionen in den ${\displaystyle \mathbb {R} ^{n}}$, die bei allen diesen Definitionen einfach komponentenweise integriert werden.

Der Integralbegriff wurde vielfältig ausgeweitet, einige Varianten sind:

• Riemann-Integral
• Daniell-Integral
• Stieltjes-Integral
• Itō-Integral und Stratonowitsch-Integral, siehe auch Diskretes stochastisches Integral
• Gauge-Integral bzw. Henstock-Kurzweil-Integral, speziell:
  • McShane-Integral
  • Pfeffer-Integral
• Maß-Integral
  • Lebesgue-Integral
  • Bochner-Integral
  • Birkhoff-Integral
  • Pettis-Integral
  • Haar-Integral
• Volkenborn-Integral

Das Haarsche Maß, nach Alfréd Haar, stellt eine Verallgemeinerung des Lebesgue-Maßes für lokalkompakte topologische Gruppen dar und induziert damit auch ein Integral als Verallgemeinerung des Lebesgue-Integrals.

Siehe: Integration von Differentialformen

Schließlich kann Integration auch dazu verwendet werden, Oberflächen von gegebenen Körpern zu messen. Dies führt in das Gebiet der Differentialgeometrie.

• Algebraische Integration
• Stochastische Integration
• Tabelle von Ableitungs- und Stammfunktionen
• Volkenborn-Integral
• Formelsammlung Analysis

• Schulbücher:
  • Integralrechnung ist ein zentraler Unterrichtsgegenstand in der Sekundarstufe II und wird somit in allen Mathematik-Lehrbüchern behandelt.
• Lehrbücher für Studenten der Mathematik und benachbarter Fächer (Physik, Informatik):
  • Herbert Amann, Joachim Escher: Analysis I, II, III. Birkhäuser-Verlag Basel Boston Berlin, ISBN 3-7643-7755-0, ISBN 3-7643-7105-6, ISBN 3-7643-6613-3.
  • Richard Courant: Vorlesungen über Differential- und Integralrechnung 1, 2. Springer, 1. Aufl. 1928, 4. Aufl. 1971.
  • Gregor Michailowitsch Fichtenholz: Differential- und Integralrechnung I–III. Verlag Harri Deutsch, Frankfurt am Main, 1990–2004. ISBN 978-3-8171-1418-4 (kompletter Satz).
  • Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. 7. Aufl. Vieweg-Verlag, 2004. ISBN 3-528-67224-2.
  • Otto Forster: Analysis. Band 3: Maß- und Integrationstheorie, Integralsätze im Rⁿ und Anwendungen, 8. verbesserte Auflage. Springer Spektrum, Wiesbaden, 2017, ISBN 978-3-658-16745-5.
  • Konrad Königsberger: Analysis. 2 Bände, Springer, Berlin 2004.
  • Wladimir Iwanowitsch Smirnow: Lehrgang der höheren Mathematik (Teil 1–5). Verlag Harri Deutsch, Frankfurt am Main, 1995–2004. ISBN 978-3-8171-1419-1 (kompletter Satz).
  • Steffen Timmann: Repetitorium der Analysis 1, 2. 1. Auflage. Binomi Verlag, 1993.
• Lehrbücher für Studenten mit Nebenfach/Grundlagenfach Mathematik (zum Beispiel Studenten der Ingenieur- oder Wirtschaftswissenschaften):
  • Rainer Ansorge und Hans Joachim Oberle: Mathematik für Ingenieure. Band 1. 3. Auflage. Wiley-VCH, 2000.
  • Lothar Papula: Mathematik für Naturwissenschaftler und Ingenieure. Band 1. 13. Auflage. Vieweg + Teubner Verlag. ISBN 978-3-8348-1749-5.
• Historisches:
  • Adolph Mayer: Beiträge zur Theorie der Maxima und Minima der einfachen Integrale. Teubner, Leipzig 1866 (Digitalisat).
  • Bernhard Riemann: Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe. Göttingen 1867 (Volltext), mit der Erstdefinition des Riemann-Integrals (Seite 12 ff.).

• Online-Rechner zur Berechnung von Integralen (Stammfunktionen) mit Rechenweg und Erklärungen (deutsch)
• mathe-online.at – Ressourcen zum Thema Integrieren (Sekundarstufe 2/FHS/Uni)
• Anschauliche Erklärungen
• The Integrator – Englische Seite zur Berechnung von Integralen
• Integralrechner – Deutsche Seite zur Berechnung von bestimmten sowie unbestimmten Integralen (Stammfunktionen)
• Teil 1 einer dreiteiligen Serie über Mehrfachintegrale (detailliert+umfangreich)
• 50 Stammfunktionsbeispiele von Funktionen
• Video: Integral, Stammfunktion. Jörn Loviscach 2010, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/9752.
• Video: Ableitung, Integral, Zufall. Jörn Loviscach 2010, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/9736.
• Video: bestimmtes Integral 1. Jörn Loviscach 2010, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/9755.
• Video: bestimmtes Integral 2. Jörn Loviscach 2010, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/9756.
• Mehrfachintegrale kann WolframAlpha.com berechnen.^[2][3]

1. ↑ D. Fremlin: The McShane and Birkhoff integrals of vector-valued functions. (Memento vom 28. April 2015 im Internet Archive).
2. ↑ Wolfram|Alpha Widgets: "Double Integral Calculator" - Free Mathematics Widget. Abgerufen am 5. Mai 2023. 
3. ↑ Wolfram|Alpha Widgets: "Triple Integral Calculator" - Free Mathematics Widget. Abgerufen am 5. Mai 2023.