| Gray-Code | |
|---|---|
| stetig | ja |
| Hamming-Abstand | 1 |
Der Gray-Code ist eine spezielle Art der Codierung, bei der sich benachbarte Zahlen nur in einer einzigen Stelle unterscheiden. Dies bedeutet, dass beim Wechsel von einer Zahl zur nächsten nur ein Bit (eine binäre Ziffer) geändert wird. Diese Eigenschaft hilft, Übertragungsfehler zu reduzieren, insbesondere bei digitalen Signalen, die sich schnell ändern. So können unterschiedliche Laufzeiten in mehradrigen Kabeln keinen Einfluss auf die Datenübertragung haben.
Der Gray-Code wurde ursprünglich für elektromechanische Sensoren und Schalter entwickelt, die anfällig für Fehler sind. Heute wird dieser Code auch in modernen digitalen Übertragungssystemen eingesetzt, wie zum Beispiel im digitalen Fernsehen (DVB-T) und im Kabelfernsehen. Der Code ist nach dem US-amerikanischen Physiker Frank Gray benannt, der 1953 das Patent für dieses Verfahren erhielt.[1]
Generierung
[Bearbeiten | Quelltext bearbeiten]Beginne mit einer Binärzahl, die nur aus Nullen besteht. Ändere dann immer die am weitesten rechts stehende Ziffer (das niederwertigste Bit) von 0 zu 1 oder umgekehrt, solange dadurch keine Kombination entsteht, die bereits vorkam.
Eine alternative Methode, die leichter zu merken und anzuwenden ist, besteht aus folgenden Schritten:[2]
- Beginne mit dem einfachsten Gray-Code-Werten: 0 und 1.
- Ergänze die Codefolge mit den gespiegelten vorhandenen Werten (schreibe sie in umgekehrter Reihenfolge auf).
- Setze vor die ursprünglichen Werte eine 0, vor die gespiegelten eine 1.
- Wiederhole Schritte 2 und 3, bis die gewünschte Länge erreicht ist.
Der so erzeugte Code hat die Eigenschaft, dass sich niederwertige Bits häufiger ändern als höherwertige. Es kann aber auch ein balancierter Gray-Code konstruiert werden, in dem sich alle Stellen (Bits) der Codewörter gleich häufig von benachbarten Codewörtern unterscheiden. Beim Durchgehen aller Codewörter in korrekter Reihenfolge ändert sich dann jede Stelle gleich oft.[3]
Der Gray-Code wird hauptsächlich als Binärcode verwendet, kann jedoch auch für mehrstufige Übertragungswege eingesetzt werden.
Logische Operatoren
[Bearbeiten | Quelltext bearbeiten]Die folgenden Punkte zeigen, wie man Schritt für Schritt aus einem Binärcode eine Gray-codierte Binärzahl erhält:
- X1: Dualzahl im Binärcode
- X2: Rechts-Shift der Dualzahl um 1 Bit
- X3: Modulo-2-Addition (XOR-Verknüpfung) von X1 und X2; dies ist die gewünschte Zahl im Graycode.
Das gleiche als Pseudocode:
- Binärcode X1 → Graycode: X3 = (X1 XOR X2)
oder anders ausgedrückt:
- Binärcode X1 → Graycode: X3 = (X1 XOR (X1 SHR 1))
wobei SHR der rechts Shiften Operator ist.
Und als Formel:
Generatormatrix
[Bearbeiten | Quelltext bearbeiten]Da der Gray-Code ein linearer Code ist, kann man ihn mit einer Generatormatrix erzeugen. Ein binäres Wort der Länge kann man als Vektor eines -dimensionalen -Vektorraums betrachten. Sei nun ein Zeilenvektor, dann lässt sich die Kodierung des Wortes in das Codewort wie folgt darstellen:
Die Dekodierung erfolgt mit der Multiplikation der Inversen von . Diese hat folgende Form:
Der Vektorraum lässt sich anschaulich mit Hyperwürfeln darstellen.
Gray-Zähler
[Bearbeiten | Quelltext bearbeiten]Man kann auch direkt einen Gray-Code-Zähler in Hardware (z. B. in HDL) programmieren. Hierzu ist es hilfreich, ein Hilfsregister zu benutzen, das mit jedem Taktzyklus toggelt.
Qh [n+1] = !Qh [n] Qh [0 ] = 0 wenn der Gray-Code-Zähler mit Null startet also Q[0]=0, oder Q[0] eine gerade Anzahl an Einsen hat. Bei anderer Initialisierung würde der Zähler rückwärts laufen.
Damit wird die Kombinatorik recht übersichtlich:
Q0 [n+1] = !(Q0 [n] ^ Qh [n] )
Q1 [n+1] = Q1 [n] ^ ( Q0 [n] & Qh [n] )
Q2 [n+1] = Q2 [n] ^ ( Q1 [n] & !Q0 [n] & Qh [n] )
Q3 [n+1] = Q3 [n] ^ ( Q2 [n] & !Q1 [n] & !Q0 [n] & Qh [n] )
…
Qk-1[n+1] = Qk-1[n] ^ ( Qk-2[n] & !Qk-3[n] & … & !Q1 [n] & !Q0 [n] & Qh [n])
Qk [n+1] = Qk [n] ^ (!Qk-2[n] & … & !Q1 [n] & !Q0 [n] & Qh [n])
Der Unterschied zwischen den Formeln für das größte Bit Qk und den kleineren Bits Qk-1 ist nötig, damit der Zähler zyklisch ist, also der Zähler nach dem letzten Wert Q=100…00 auf den Anfangswert Q=000…00 springt. Bei einem unendlichen Zähler gäbe es keinen Unterschied.
^ := Exklusiv Oder / XOR / Antivalenz
! := Inverter / NOT / Negation
& := Und / AND / Konjunktion
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]Die Hamming-Distanz benachbarter Codewörter ist 1, d. h. die Werte unterscheiden sich in genau einem Bit. Das ist das höchstwertige Bit, das sich in der Binärdarstellung der mit 0 beginnenden Zeilennummern ändert. Zum Beispiel haben Zeile 11 und Zeile 12 die Binärdarstellungen 001011 und 001100. Es ändern sich also die letzten drei Bits. Die Codewörter von Zeile 11 und 12, nämlich 001110 und 001010, unterscheiden sich daher im drittletzten Bit.
Die absolute Differenz benachbarter Codewörter ist also eine Zweierpotenz. Diese Zweierpotenz ist die größte Zweierpotenz, durch die sich die Zeilennummer des zweiten Codeworts teilen lässt. Ist der größte ungerade Teiler der Zeilennummer von der Form 4k + 1, also 1, 5, 9, ..., dann ist die Differenz positiv. Ist der größte ungerade Teiler von der Form 4k + 3, also 3, 7, 11, ..., dann ist die Differenz negativ. Zum Beispiel hat die Zeile 12 die Zahl 22 = 4 als größte Zweierpotenz und die Zahl 3 als größte ungerade Teiler. Die Differenz der Codewörter von Zeile 11 und Zeile 12 ist also gleich −4.
Bedeutung
[Bearbeiten | Quelltext bearbeiten]Ein Ziffernschritt sei nachfolgend der kleinstmögliche Unterschied, die kleinste Differenz, das kleinste Intervall zwischen zwei digitalisierten Werten. Eine zeitliche Veränderung eines Zahlenwertes um einen Ziffernschritt wird nachfolgend als stetige Veränderung bezeichnet. Signale werden über Datenübertragungsstrecken übertragen. Typische Signalgeber sind z. B. Signale eines Temperatursensors oder eines Drehwinkelgebers.
Die Motivation für die Entwicklung dieses Codes ist das folgende Problem: Signalübertragungsstrecken und Signalgeber unterliegen Störeinflüssen, die dazu führen können, dass sich einzelne oder mehrere Stellen eines Codewortes (codierte Zahl) unbeabsichtigterweise verändern oder falsch interpretiert werden können. Physische Schalter sind beispielsweise nicht ideal. Es ist sehr unwahrscheinlich, dass physische Schalter ihren Zustand exakt synchron ändern.
Auf mehreren Adern einer elektrischen Datenleitung sollen nun beispielsweise Daten parallel übertragen werden, die sich stetig ändern. Als Dualzahl übertragen, ändern sich die Bits bei einem neuen Messwert auf jeder betroffenen Leitung theoretisch exakt gleichzeitig, und zwar sowohl am Eingang der Leitung als auch am Ausgang. Tatsächlich aber ändern sich die Bits auf der Leitung nicht gleichzeitig. Das kann verschiedene Ursachen haben: Bauteilestreuung, Laufzeiten, Asymmetrien usw. Dadurch kommt es zu ungewollten Zwischenzuständen und kurzzeitig (zwischen den roten Linien) falsch empfangenen Werten:
|
|
Problem bei Dualcode-Signalen
[Bearbeiten | Quelltext bearbeiten]Erklärung zu den Abbildungen:
Als steigende Flanke wird nachfolgend der Übergang vom Wert 0 („Aus“) auf 1 („Ein“) eines Signals auf einer Datenleitung bezeichnet. In der oberen Abbildung sind theoretische Dualcode (BCD) Signale auf vier parallelen Leitungen dargestellt sowie reale Dualcode Signale in der Abbildung darunter wie sie in der Praxis auftreten können. Die realen Signale auf der Leitung 1 sind im Vergleich zu dem theoretischen Signal zeitlich verschoben. Die erste steigende Flanke des realen Signals auf Datenleitung 1 kommt hier im Vergleich zu dem theoretischen Signal um das Zeitintervall t2−t1 später am Ausgang an, während die zweite steigende Flanke um das Intervall t4−t3 früher am Ausgang anliegt. Die Signale „0“ und „1“ auf den Leitungen werden nachfolgend als Tetrade (vier-stelliges Codewort) geschrieben, wobei der Kanal 3 an der Stelle ganz links und der Kanal 0 an der Stelle ganz rechts notiert wird. Die dazugehörigen Werte, die theoretisch vor der Codierung bei dem Signalgeber vorhanden waren, lauten im Dezimalsystem: 0, 1, 2, 3, 4, 5, 6, 7 usw. Die Werte des Gebers ändern sich in diesem Beispiel also stetig, das heißt immer nur um das kleinstmögliche Intervall von 1, also ohne größere Sprünge zwischen zwei aufeinanderfolgenden Werten.
Während das theoretische Signal in der Reihenfolge
- {0000}, {0001}, {0010}, {0011}, {0100}, {0101}, {0110}, {0111} usw.
abgesendet wird, kommen am Ausgang des realen Signals kurzzeitig andere Signalzustände an:
- {0000}, {0001}, {0000}, {0010}, {0011}, {0100}, {0101}, {0111}, {0110}, {0111} usw.
Während sich der Dezimalwert des Gebers zwischen zwei aufeinanderfolgenden Werten theoretisch maximal um 1 ändert, entsteht hier auf der Empfängerseite verursacht durch einen Laufzeitfehler ein Sprung mit einem Betrag von 2 (dezimal) und zwar verursacht durch die Signalfolge {0000} und {0010}, die der Zahlenfolge 0 und 2 im Dezimalsystem entspricht. Ein weiterer Sprung um den Betrag von 2 (dezimal) entsteht durch die Signalfolge {0101} und {0111} (dezimal: 5 und 7). Der theoretisch richtige Dezimalwert des Gebers betrug 3 zwischen den Zeitpunkten t1 und t2. Der Laufzeitfehler des realen Signals führt allerdings dazu, dass der Wert in diesem Intervall als 1 interpretiert wird. Der Betrag des Fehlers zwischen theoretischem und realem gestörten Signal beträgt also zwei, wie auch der Fehler zwischen den Zeitpunkten t3 und t4.
Lösung mit Gray-Code
[Bearbeiten | Quelltext bearbeiten]Die theoretischen Ausgangswerte des Signalgebers lauten wie oben im Dezimalsystem: 0, 1, 2, 3, 4, 5, 6, 7 usw. Die Dezimalwerte sind allerdings nun mithilfe des Gray-Codes codiert bzw. werden mithilfe des Gray-Codes gesendet. Zwischen zwei aufeinanderfolgenden Eingangswerten ändert sich dabei immer nur ein Bit (eine Stelle im Codewort):
- Abgesendete Sequenz: {0000}, {0001}, {0011}, {0010}, {0110}, {0111}, {0101}, {0100} usw.
- Ankommende Sequenz: {0000}, {0001}, {0011}, {0010}, {0110}, {0111}, {0101}, {0100} usw.
Hier kommt also am Ausgang auch dann die gleiche Sequenz wie am Eingang an, wenn beachtliche Zeitfehler (rote Linien) auftreten.
Die gestörte Tetrade zwischen den Zeitpunkten t1 und t2 lautet hier {0001}, die anstatt dem theoretischen Codewort {0011} empfangen worden ist, was im Dezimalsystem dem Empfang einer 1 anstatt der 2 entspricht. Die gestörte Tetrade zwischen den Zeitpunkten t3 und t4 lautet {0101}, anstatt dass {0111} empfangen worden ist. Das entspricht dezimal dem Empfang einer 6 anstatt 5.
Der Dezimalbetrag des Fehlers zwischen dem „wahren“ Wert des Gebers im Vergleich zu dem gestörten Signal entspricht bei Verwendung des Gray Codes also nur 1 und ist somit geringer als im oberen Beispiel, bei dem der Dezimalwert des Gebers BCD (dual) codiert wurde.
Abweichungen an einer oder wenigen Stellen eines Codewortes werden bei der Verwendung des Gray Codes also zwar nicht erkannt, resultieren aber nicht in gravierenden Abweichungen des ursprünglichen Eingangswertes. Die Verwendung des Gray Codes erlaubt auch keine Fehlerkorrektur.
Karnaugh-Veitch-Diagramm
[Bearbeiten | Quelltext bearbeiten]Im Karnaugh-Veitch-Diagramm erkennt man den Graycode – es sind mehrere Sequenzen möglich – daran, dass Übergänge nur zwischen (horizontal oder vertikal) benachbarten Feldern vorkommen.
|
|
Der Code eignet sich auch für zyklische Anwendungen wie der unten abgebildeten Scheibe, da sich auch beim Übergang von der höchsten Zahl auf die Null nur eine Stelle ändert.
Die Wertigkeit einer 1 an der Position im Gray-Code Zahlensystem ist (wobei n ab 1 zählt, also … 31, 15, 7, 3, 1). Die einzelnen Einsen werden, im Gegensatz zum normalen Binärsystem, nicht addiert, sondern von rechts beginnend subtrahiert. Beispiel: 111Gray = 7 − (3 − 1) = 5 oder 1111Gray = 15 − (7 − (3 − 1)) = 10. Stellen, die 0 sind, werden dabei ausgelassen, Beispiel: 101Gray = 7 − 1 = 6.
Bei der Generierung von Gray-Code wird symmetrisch vorgegangen.
Da sich benachbarte Werte nur in einer Ziffer unterscheiden, ist der Gray-Code geeignet, um Fehler in seriellen Prozessen aufzudecken.
Programmierung
[Bearbeiten | Quelltext bearbeiten]Folgendes Beispiel zeigt eine Implementierung in der Programmiersprache C++, die die Zeilen des Gray-Codes mit 6 Bits iterativ erzeugt und auf der Konsole ausgibt.[4][5]
#include <iostream>
#include <string>
#include <vector>
using namespace std;
void writeGrayCode (int const bits) // Diese Funktion erzeugt den bits-Bit-Gray-Code und gibt ihn auf der Konsole aus
{
vector<string> GrayCode {""}; // Ergebnis-Vektor mit initialer leerer Zeile
// Diese for-Schleife wird bits-mal durchlaufen und erzeugt iterativ die Text für den 1-Bit-, 2-Bit-, ..., n-Bit-Gray-Code.
// Die Schleifenvariable pos durchläuft die jeweiligen Bitpositionen 1, 2, 4, ..., 2^(n-1)
for (int pos = 1; pos < (1 << bits); pos *= 2)
{
for (int i = pos; --i >= 0; ) // Hänge die zuletzt erzeugten Zeilen in umgekehrter Reihenfolge am Ende noch mal an.
GrayCode.push_back (GrayCode[i]); // Die Anzahl der Zeilen verdoppelt sich dadurch.
for (int i = 0*pos; i < 1*pos; i++) // Füge eine '0' am Anfang der Zeilen der ersten Hälfte hinzu.
GrayCode[i] = "0" + GrayCode[i];
for (int i = 1*pos; i < 2*pos; i++) // Füge eine '1' am Anfang der Zeilen der zweiten Hälfte hinzu.
GrayCode[i] = "1" + GrayCode[i];
}
for (auto & E : GrayCode) // Diese for-Schleife durchläuft alle Zeilen des Gray-Code
cout << E << endl; // Ausgabe auf der Konsole
}
int main() // Eintrittspunkt beim Aufruf eines C++-Programms
{
writeGrayCode(6); // Aufruf der Funktion, die hier den 6-Bit-Gray-Code erzeugt und auf der Konsole ausgibt
}
Zwei- und mehrdimensionale Graycodes
[Bearbeiten | Quelltext bearbeiten]In mehrdimensionalen Vektorräumen sind mehrdimensionale Graycodes möglich. In -dimensionalen Graycodes mit jeweils Codeworten pro Dimension hat jedes Codewort Nachbarn in Richtungen, die sich um maximal 1 Bit unterscheiden. In -dimensionalen Graycodes mit jeweils Codeworten pro Dimension hat jedes Codewort Nachbarn in Richtungen (die entgegengesetzten Nachbarn sind die gleichen), die sich um maximal 1 Bit unterscheiden.
Genutzt werden diese in der Digitalen Kodierung, siehe hier.
Geometrische und graphentheoretische Darstellung
[Bearbeiten | Quelltext bearbeiten]-
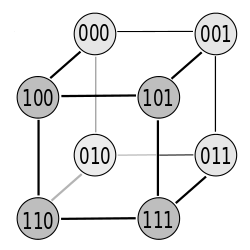
Bild 1: 3-Bit-Gray-Code als Ecken eines (3D-)Würfels
-
Bild 2: Koordinatensystem hinzugefügt
Bild 1 zeigt den Hexaeder für 3 Variablen und Bild 2 den gleichen Würfel mit dazugehörigem Koordinatensystem. Die Knoten (Eckpunkt oder Kreise) am Einheitswürfel entsprechen jeweils einer Zeile im Gray-Code. Die Übergänge (Nachbarschaft der Zeilen) sind durch die Kanten des Würfels symbolisiert. Beim Wandern auf der Kante entsteht ein Gray-Code.
geschlossener 3-Bit-Gray-Code a) b) c) d) e) f) 000 000 000 000 000 000 001 100 010 010 001 100 101 101 110 011 011 110 100 001 100 001 010 010 110 011 101 101 110 011 111 111 111 111 111 111 011 110 011 110 101 101 010 010 001 100 100 001
-
Bild 3: Die 6 Pfade zu dem Gray-Code in der Tabelle. Es handelt sich um einen Hamiltonkreis. Startpunkt: 000 (grüner Kreis jeweils hinten links oben), Verlauf: grüne→blaue→rote→schwarze Linie, Endpunkt: am Startpunkt
Fehler in Bild b) Linie 101→111 und in Bild d) 011→111
Auf jeder Kante ändert sich genau 1 Bit. Der Gray-Code hat so viel Nachbarschaften, wie der Würfel Kanten hat. Aus dem Würfel in Bild 1 können die möglichen Pfade auf 6 verschiedenen Wegen durchschritten werden. Somit ergeben sich 12 Möglichkeiten (jeder Weg vorwärts und rückwärts), um einen 3-Bit-Gray-Code zu erzeugen, der die Bedingungen des Gray-Codes erfüllt (Tabelle und Bild 3). Abgesehen davon ist der Gray-Code zyklisch und der Startpunkt könnte deshalb auch an einer anderen Zeile sein. Wegen seiner einfachen rekursiven Generierungsvorschrift wird meist der binäre reflektierte Gray-Code (binary-reflected Gray code) angegeben (Spalte „e“ – vorletzte Spalte in der Tabelle). Es gibt für eine bestimmte Bitlänge eine ganze Klasse von Graycodes.
Es gibt für einen n-Bit-Gray-Code exakt so viel Varianten, wie es Hamiltonkreise auf einem n-dimensionalen Hyperwürfel gibt. Die Anzahl dieser Hyperwürfel ist in der On-Line Encyclopedia of Integer Sequences als Sequenz A003042 angegeben und (Stand Februar 2022) bis zu 6 Dimensionen bekannt.[6]
Für 1 bit gibt es 1 möglichen Gray-Code, für 2 bit gibt es 2 mögliche Gray-Codes und für 3 bit gibt es 12 mögliche Gray-Codes:
Nr. 1 0 1
Nr. 1 00 01 11 10 Nr. 2 00 10 11 01
Nr. 1 000 001 011 010 110 111 101 100 Nr. 2 000 001 011 111 101 100 110 010 Nr. 3 000 001 101 100 110 111 011 010 Nr. 4 000 001 101 111 011 010 110 100 Nr. 5 000 010 011 001 101 111 110 100 Nr. 6 000 010 011 111 110 100 101 001 Nr. 7 000 010 110 111 011 001 101 100 Nr. 8 000 010 110 100 101 111 011 001 Nr. 9 000 100 101 111 110 010 011 001 Nr. 10 000 100 101 001 011 111 110 010 Nr. 11 000 100 110 111 101 001 011 010 Nr. 12 000 100 110 010 011 111 101 001
Darüber steigt die Zahl steil an:
Für 4 bit sind es 2688, für 5 bit 1813091520 und für 6 bit 71676427445141767741440.
Balancierte Gray-Codes
[Bearbeiten | Quelltext bearbeiten]Ein balancierter Gray-Code ist ein Gray-Code, bei dem sich die Anzahl der Änderungen für alle Bits höchstens um 2 unterscheidet. Wenn und die Anzahl der Änderungen für die Bits mit den Indizes und ist, dann gilt für jeden balancierten Gray-Code die Ungleichung .
Ein balancierter Gray-Code mit Bits kann folgendermaßen konstruiert werden:
- Aus einem beliebigen -Bit Gray-Code mit den Zeilen wird eine Teilfolge ausgewählt, wobei gerade ist und , und , direkt aufeinanderfolgende Zeilen sind.
- Die vier Kopien des -Würfels. In jedem dieser Würfel betrachtet man den definierten Gray-Code mit den Zeilen und löscht die Übergänge zwischen direkt aufeinanderfolgenden Zeilen auf folgende Weise: Aus werden die entsprechenden Elemente von den Zeilen mit ungeraden Indexen gelöscht. Aus werden die entsprechenden Elemente von gelöscht. Aus werden die entsprechenden Elemente von den Zeilen mit geraden Indexen gelöscht. Aus wird nur das entsprechenden Elemente von gelöscht.
- Die vier Teilwürfel werden miteinander verbunden.
Es kann überprüft werden, dass die oben beschriebene Konstruktion tatsächlich einen balancierten -Bit-Gray-Code ergibt. Die Verteilung der Anzahl der Änderungen für die Bits in diesem Code hängt von der Wahl der ausgewählten Teilfolge ab.[7]
Anwendungen
[Bearbeiten | Quelltext bearbeiten]

Eine Anwendungsmöglichkeit ist die Bestimmung der absoluten Position einer Scheibe oder Leiste, die mit schwarzen und weißen Balken markiert ist. Die Balken werden mit Lichtschranken oder anderen Sensoren abgetastet. Diese Position wird dann zur Winkel- oder Drehgeschwindigkeitsmessung verwendet.[8]
Eine weitere Anwendung ist die Streifenprojektion. Dort wird eine Folge von Mustern aus parallelen Streifen auf ein Objekt projiziert. Die Nummer der Streifen ist Gray-kodiert und kann von einer beobachtenden Kamera für jeden Bildpunkt berechnet werden.
Eine andere Anwendung ist das asynchrone Einlesen von Daten. Beispielsweise wird der Gray-Code genutzt, um in Korrelatoren die Zählerstände fehlerfrei einzulesen. Selbst im ungünstigsten Fall, wenn während eines kippenden Bits eingelesen wird, ist das Ergebnis immer korrekt, da ein kippendes Bit nicht definiert ist und es zudem nur einen Unterschied von ±1 ausmacht. Diese Art des Einlesens erfordert keine Synchronisation.
Weitere Anwendungsmöglichkeiten sind Windrichtungsmesser oder Wasserniveaumesser, Abbildung des Fahrkorbstands bei Aufzügen.
Der reflektierte Gray-Code hat eine enge Beziehung zur Lösung des Problems der Türme von Hanoi, und er beschreibt auch den Lösungsweg der Chinesischen Ringe.
Reduktion von Bitfehlern in digital PSK-, APSK- und QAM-modulierten Signalen
[Bearbeiten | Quelltext bearbeiten]In moderner Digitale Kommunikation spielen 1D- and 2D-Gray-Codierungen eine bedeutende Rolle beim Verhindern von Mehrfachbitfehlern bei Übertragungen. Sie machen damit Fehlerkorrektur-Verfahren effizienter. Sie finden Verwendung bei allen PSK-Modulationen wie auch bei geradzahligen (22n) QAM-Modulationen. Benachbarte, durch Rauschen sehr wahrscheinlich auftretende fehlerhafte Codeworte unterscheiden sich nur um 1 Bit. Nicht perfekt lassen sie sich umsetzen bei APSK-Modulationen (z. B. APSK-16 und APSK-32) und bei ungeradzahligen (22n+1) QAM-Modulationen.
-
Codes 4-PSK
-
Codes 8-PSK
-
Codes 16-QAM
Beispiel
[Bearbeiten | Quelltext bearbeiten]Die Dezimalzahl entspricht dem Gray-Code . Die Dekodierung in die Dezimaldarstellung folgt dann der Regel . Wenn mehrere Einsen in einer Gray-Code-Zahl vorkommen, werden diese voneinander subtrahiert: Der Gray-Code wird wie folgt dekodiert: .
Allgemeines Verfahren: Bei einer Umwandlung ist entscheidend, an welcher Position die Einser stehen. Die Position hat Einfluss auf die Rechnung. Wenn wir uns die Zahl 100 anschauen, dann steht die Eins auf Position 3 (von rechts nach links). Den Faktor für die Eins bekommt man, indem man sich überlegt, welche Dezimalzahl maximal in einer 3-Bit Zahl binär gespeichert werden kann. In 3 Bit Binärcode kann maximal die Zahl 7 (111) gespeichert werden. Nehmen wir jetzt eine größere Binärzahl, funktioniert das praktisch analog. Binärzahl: 11010 (1 an Position 5,4 und 2). 5 Bit Binärzahl: max. 31 4 Bit Binärzahl: max. 15 2 Bit Binärzahl: max. 3
Berechnung:
Gray-Code zurückrechnen
[Bearbeiten | Quelltext bearbeiten]Eine Zeile des Gray-Codes kann in die Zeilennummer zurückgerechnet werden, indem alle Bits vom höchstwertigen Bit bis zum aktuellen Bit mit einem exklusiven Oder verknüpft werden. Dazu werden die Bits der Zeile mit jedem Iterationsschritt jeweils um 1 Bit nach rechts verschoben und mit dem Zwischenergebnis mit einem exklusiven Oder verknüpft.[9]
Das folgende Beispiel zeigt die Implementierung einer Funktion, die die Zeile eines (beliebigen n-Bit) binären reflektierten Gray-Codes decodiert:
int GrayDecode (int const CodeWort)
{
int res = CodeWort;
int mask = CodeWort; // Die Bitmaske ist der Gray-Code res mit einer Rechtsverschiebung der Bits
while (mask) // Solange nicht alle gesetzten Bits nach rechts verschoben sind und der Wert ungleich 0 ist ...
{
mask >>= 1; // Rechtsverschiebung um 1 Bit
res ^= mask; // Exklusives Oder mit der Bitmaske
}
return res;
}
Spezielle Gray-Codes
[Bearbeiten | Quelltext bearbeiten]Gray-Codes mit m bits und Länge kleiner als 2m
[Bearbeiten | Quelltext bearbeiten]Es existieren auch Gray-Codes mit Bits mit einer Länge von weniger als . Hierfür muss Länge gerade sein. Eine Möglichkeit, sie zu konstruieren, besteht in der Verwendung eines Standard-Gray-Codes und dem paarweisen Wegstreichen entweder des ersten und des letzten Eintrags oder von Einträgen in der Mitte[10]. Die OEIS-Folge A290772[11] zählt die Anzahl der möglichen Gray-Codes der Länge auf, wofür jeweils die minimale Anzahl von Bits verwendet werden.
Excess-Gray-Code
[Bearbeiten | Quelltext bearbeiten]Wird aus einem Gray-Code ein Ausschnitt herausgetrennt, beispielsweise die letzten 3 Bit eines 4-Bit-Gray-Codes, so erhält man einen sogenannten Excess-Gray-Code. Dieser Code zeichnet sich dadurch aus, dass die betroffenen, herausgetrennten Bits bei weiterem Hochzählen des originalen Codewortes rückwärts zählen. Dies ist dadurch bedingt, dass bei einer Gray-Codierung kein Überlauf bei der höchsten Zahl entsteht, wie man ihn aus dem klassischen Binärsystem kennt.[12]
Beispiel: Die höchste mit einem 3-Bit-Gray-Code codierte Zahl, also 7, wird als (0)100 repräsentiert. Weiteres Addieren einer 1 resultiert in einer 8, im Gray-Code 1100. Die letzten 3 Bit erfahren keinen Überlauf und verhalten sich bei weiterem Hochzählen genau entgegengesetzt zur ursprünglichen Zählrichtung.
Bei Sensoren, die mehrere Werte seriell als Gray-codierte Werte ausgeben, sollte daher darauf geachtet werden, ob es sich um einen zusammengesetzten Gray-Code oder um separate Codeworte handelt, da die ausgegebenen Werte sonst den Anschein erwecken, der Sensor würde rückwärts zählen.
Geschichte
[Bearbeiten | Quelltext bearbeiten]Noch bevor die Bezeichnung Gray-Code eingeführt wurde, gab es bereits mathematische Knobelspiele, in denen das Prinzip angewendet wurde. Erst später fand der Code die Beachtung von Ingenieuren. Bereits 1874 wendete Otto Schäffler, der in Wien Telegrafen und Telefone produzierte und verbesserte, den reflektierten Gray-Code an. Der Franzose Jean-Maurice-Émile Baudot verwendete Gray-Codes im Jahr 1874 für die elektrische Telegrafie. Er erhielt für seine Arbeit die Auszeichnung der französischen Ehrenlegion.
Namensgebend war allerdings Frank Gray, Forscher in den Bell Laboratories, der den schon 1941 von George Stibitz beschriebenen Code[13] im Jahre 1947 für seine Zwecke wiederentdeckte. Unter dem Titel Pulse Code Communications wurde im Jahre 1953 ein Patent für eine Gray-kodierende Elektronenröhre erteilt.[1]
Ähnliche Codes
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Robert W. Doran: The Gray Code. In: Journal of Universal Computer Science. Band 13, Nr. 11, 2007, S. 1573–1597 (karadimov.info [PDF; 219 kB]).
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Java-Beispiel für die Umwandlung einer Dezimalzahl in Gray-Code Darstellung ( vom 30. September 2007 im Internet Archive)
- Algorithmen zur Erzeugung des reflektierten Gray-Codes auf dem Combinatorial Object Server
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ a b Patent US2632058A: Pulse code communication. Angemeldet am 13. November 1947, veröffentlicht am 17. März 1953, Anmelder: Bell Telephone Labor Inc, Erfinder: Frank Gray.
- ↑ EE Times: Gray Code Fundamentals – Part 2
- ↑ Girish S. Bhat, Carla D. Savage: Balanced Gray Codes. In: The Electronic Journal of Combinatorics. 28. August 1996, ISSN 1077-8926, S. R25–R25, doi:10.37236/1249 (combinatorics.org [abgerufen am 22. Mai 2021]).
- ↑ GeeksforGeeks: Generate n-bit Gray Codes
- ↑ Rosetta Code: Gray code
- ↑ A003042: Number of directed Hamiltonian cycles (or Gray codes) on n-cube. (Formerly M2053)
- ↑ Girish S. Bhat, Carla D. Savage, North Carolina State University: Balanced Gray Codes
- ↑ Robert W. Doran: The Gray Code. In: Journal of Universal Computer Science. Band 13, Nr. 11, 2007, S. 1575, 1577.
- ↑ Lénárd Szolnoki's programming site: Implementations for Gray code encoding and decoding
- ↑ Max Maxfield: How to generate Gray Codes for non-power-of-2 sequences. 29. Juni 2007, abgerufen am 25. Februar 2023 (englisch).
- ↑ A290772: Number of cyclic Gray codes of length 2n which include all-0 bit sequence and use the least possible number of bits.
- ↑ AutomationDirect: What are Excess Gray Codes?
- ↑ Patent US2307868A: Binary counter. Angemeldet am 26. November 1941, veröffentlicht am 12. Januar 1943, Anmelder: Bell Telephone Labor Inc, Erfinder: George R. Stibitz.