Als Clipping oder Abschneiden (englisch to clip = „abschneiden“, „kappen“) bezeichnet man in der Computergrafik das Abschneiden von Grundobjekten am Rand eines gewünschten Bildschirmausschnittes oder Fensters. Ein Fenster kann dabei ein beliebiges Polygon sein.

Gegeben sind die beiden Endpunkte einer Strecke ${\displaystyle P=(x_{p},y_{p}),Q=(x_{q},y_{q})\in \mathbb {R} ^{2}}$ und ein Fenster ${\displaystyle \Omega =[x_{\min },x_{\max }]\times [y_{\min },y_{\max }]\subset \mathbb {R} ^{2}}$. Ziel ist es nun, den Teil der Strecke ${\displaystyle {\overline {PQ}}}$ zu bestimmen, der sich innerhalb des Rechteckfensters befindet.

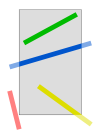
Es sind vier Fälle möglich:

• ${\displaystyle P}$ und ${\displaystyle Q}$ liegen im Rechteckfenster. Die gesamte Gerade ist zu zeichnen (grüne Strecke).
• ${\displaystyle P}$ und ${\displaystyle Q}$ liegen außerhalb des Rechteckfensters, die Gerade verläuft zum Teil jedoch durch das Rechteckfenster. Die beiden Schnittpunkte müssen berechnet werden und der Teil zwischen den beiden Schnittpunkten ist zu zeichnen (blaue Strecke).
• ${\displaystyle P}$ oder ${\displaystyle Q}$ liegt im Fenster und der jeweils andere Punkt außerhalb. In diesem Fall wird der Teil vom im Fenster liegenden Punkt bis zum Schnittpunkt mit der Fensterkante gezeichnet (gelbe Strecke).
• ${\displaystyle P}$ und ${\displaystyle Q}$ liegen so außerhalb des Fensters, dass nichts zu zeichnen ist (rote Strecke).

Solche Probleme lösen die Algorithmen von Cohen-Sutherland, Cyrus-Beck und von Liang-Barsky.

Es liegt wiederum eine Strecke mit Endpunkte ${\displaystyle P}$ und ${\displaystyle Q}$ wie oben vor. Zur Berechnung der Anteile, die innerhalb eines Polygons liegen, werden die Schnittpunkte der Strecke mit dem Polygonfenster unter Berücksichtigung des Inside Test und des Max-Min Test bestimmt. Diese Vorgehensweise vollzieht der Scanline-Algorithmus zum zeilenweisen Zeichnen von Polygonen. Es werden Zeile für Zeile Punkte ${\displaystyle P}$ und ${\displaystyle Q}$ mit ${\displaystyle y_{p}=y_{q}}$ gewählt, die sich links oder rechts neben den Polygon befinden. Durch Clipping dieser Linie am Polygon entsteht zeilenweise der zu zeichnende Polygonanteil einer kompletten Zeile.

Polygonclipping ist das Clipping eines beliebigen Polygons bezüglich eines Rechteckfensters oder beliebigen Polygons. Es treten verschiedene Situationen auf:

• Kanten des Polygons müssen vollständig, teilweise oder gar nicht übernommen werden,
• Neue Kanten müssen aufgenommen werden,
• Aus einem Polygon können beim Clipping mehrere Polygone entstehen.

Diese Probleme deckt der Algorithmus von Sutherland-Hodgman ab. Er betrachtet dabei ein Polygon als eine Sequenz von Punkten, die er abläuft und dann

• den Punkt übernimmt,
• den Punkt als Schnittpunkt des Polygons mit dem Fensterpolygon neu berechnet,
• den Punkt entfernt.

• Clippingebene
• Probleme beim Rastern von Linien

• Max K. Agoston: Computer Graphics and Geometric Modeling. Springer, London 2005, ISBN 1-85233-818-0.

• Übersicht über verschiedene Clipping-Algorithmen