
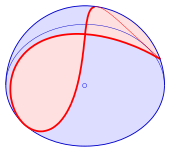
Ein vivianisches Fenster oder vivianische Kurve, benannt nach dem italienischen Mathematiker und Physiker Vincenzo Viviani, ist eine 8-förmige Kurve auf einer Kugel, die man als Schnittkurve der Kugel (Radius ) und einem die Kugel berührenden Zylinder mit Radius erzeugen kann.[1][2] (S. Bild).
Viviani stellte 1692 die Aufgabe, aus einer Halbkugel (Radius ) zwei Fenster so herauszuschneiden, dass der Rest der Halbkugelfläche „quadrierbar“ ist. Dabei bedeutet quadrierbar: Man kann mit Zirkel und Lineal ein flächengleiches Quadrat konstruieren. Es stellt sich heraus (s. unten), dass der fragliche Flächeninhalt ist.

Analytische Beschreibung
Um die Quadrierbarkeit möglichst einfach zeigen zu können, wird hier angenommen, dass
- die Kugel durch die Gleichung beschrieben wird und
- der Zylinder senkrecht steht und der Gleichung genügt.
Der Zylinder berührt die Kugel im Punkt
Eigenschaften der Kurve
Grund-, Auf- und Seitenrisse

Durch Elimination von bzw. bzw. aus den Gleichungen ergibt sich: Die orthogonale Projektion der Kurve auf die
- --Ebene ist der Kreis mit der Gleichung
- --Ebene die Parabel mit der Gleichung
- --Ebene die algebraische Kurve mit der Gleichung
Parameterdarstellung

Stellt man die Kugel mit Kugelkoordinaten
dar und setzt erhält man die Kurve
Man prüft leicht nach, dass diese Kurve nicht nur auf der Kugel liegt, sondern auch die Zylindergleichung erfüllt. Diese Kurve ist allerdings nur die eine Hälfte (rot) der Viviani-Kurve, nämlich der Teil von links unten nach rechts oben. Den anderen Teil (grün, von rechts unten nach links oben) erhält man über die Beziehung
Mit Hilfe dieser Parameterdarstellung lässt sich die Aufgabe von Viviani leicht lösen.
Quadrierbarkeit der Restfläche
Den Inhalt des rechten oberen Viertels des vivianischen Fensters (s. Bild) erhält man mittels eines Oberflächenintegrals:
Der gesamte Flächeninhalt des von der vivianischen Kurve eingeschlossenen Fläche ist also und
- der Inhalt der Halbkugel-Oberfläche () ohne dem Inhalt des vivianischen Fensters ist , also gleich dem Quadrat des Kugeldurchmessers.
Beziehung zu anderen Kurven
- Der Aufriss (s. oben) ist eine Lemniskate von Gerono.
- Die vivianische Kurve ist ein Spezialfall einer Clelia-Kurve. Bei einer Clelia-Kurve ist

Subtrahiert man von der Kugelgleichung 2× die Zylindergleichung und führt quadratische Ergänzung durch, erhält man die Gleichung
Diese Gleichung beschreibt einen senkrechten Kreiskegel mit der Spitze im Punkt , dem Doppelpunkt der vivianischen Kurve. Also gilt
- Die vivianische Kurve ergibt sich auch sowohl beim Schnitt
- a) der Kugel mit dem Kegel mit der Gleichung
- als auch beim Schnitt
- b) des Zylinders mit diesem Kegel.
Einzelnachweise
- ↑ Kuno Fladt: Analytische Geometrie spezieller Flächen und Raumkurven. Springer-Verlag, 2013, ISBN 3322853659, 9783322853653, S. 97.
- ↑ K. Strubecker: Vorlesungen der Darstellenden Geometrie. Vandenhoeck & Ruprecht, Göttingen 1967, S. 250.
































