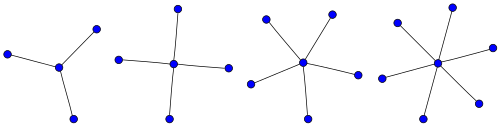
Ein Sterngraph, kurz Stern, ist in der Graphentheorie eine Klasse von Graphen einfacher Struktur. In einem Sterngraph ist ein zentraler Knoten mit allen anderen Knoten durch Kanten verbunden, während die anderen Knoten neben diesem zentralen Knoten keine weiteren Nachbarn besitzen. Sterngraphen mit Kanten werden mit oder bezeichnet. Eine Netzwerktopologie in Form eines Sterngraphen wird Stern-Topologie genannt.
Definition
Ein Sterngraph , auch -Stern genannt, ist ein ungerichteter Graph bestehend aus den Knoten
und den Kanten
- ,
wobei meist angenommen wird. Der Knoten wird Zentrum des Sterns, zentraler Knoten oder Sternknoten genannt. Gelegentlich wird ein Sterngraph mit Knoten auch mit bezeichnet.[1]
Eigenschaften
Im Folgenden werden nur Sterngraphen bestehend aus mindestens drei Knoten betrachtet.
- Ein Sterngraph ist ein Baum, also ein zusammenhängender azyklischer ungerichteter Graph ohne Mehrfachkanten. Meist wird als Wurzel des Baums der zentrale Knoten gewählt; der Baum hat dann die Höhe eins.[2]
- Ein Sterngraph ist ein vollständig bipartiter Graph , bei dem die eine Partitionsklasse aus dem zentralen Knoten und die andere Partitionsklasse aus den übrigen Knoten besteht.[3]
- Der Durchmesser ist zwei und der mittlere Abstand zwischen zwei Knoten mit etwas kleiner als zwei.[4]
- Der Kantengraph des Sterngraphen ist der vollständige Graph . Umgekehrt gibt es keinen Graphen, dessen Kantengraph ein Sterngraph mit mehr als drei Knoten ist.[5]
- Die chromatische Zahl eines Sterngraphen ist zwei. Eine zulässige Färbung erhält man, indem man den zentralen Knoten in einer Farbe und die übrigen Knoten in der anderen Farbe färbt. Das chromatische Polynom des Sterngraphen ist .[6]
- Jeder Sterngraph besitzt zwei graziöse Beschriftungen: bei der einen wird der zentrale Knoten mit , bei der anderen mit beschriftet; die übrigen Knoten erhalten jeweils die verbleibenden Zahlen zwischen und .[7]
- Die peripheren Knoten eines Sterngraphen bilden eine maximale stabile Menge des Graphen. Die Stabilitätszahl des Sterngraphen ist daher .[8]
Siehe auch
Literatur
- Peter Tittmann: Graphentheorie: Eine anwendungsorientierte Einführung. Hanser Verlag, 2003, ISBN 3-446-22343-6.
- Walter D. Wallis: A Beginner's Guide to Graph Theory. 2. Auflage. Springer, 2007, ISBN 0-8176-4484-9.
Einzelnachweise
- ↑ Eric W. Weisstein: CRC Concise Encyclopedia of Mathematics. 2. Auflage. CRC Press, 2010, S. 2838.
- ↑ Wallis: A Beginner's Guide to Graph Theory. 2007, S. 53.
- ↑ Tittmann: Graphentheorie: Eine anwendungsorientierte Einführung. 2003, S. 23.
- ↑ Robert Sedgewick, Kevin Wayne, Kevin Wayne: Einführung in die Programmierung mit Java. Pearson, 2011, S. 693–694.
- ↑ Tittmann: Graphentheorie: Eine anwendungsorientierte Einführung. 2003, S. 69.
- ↑ Wallis: A Beginner's Guide to Graph Theory. 2007, S. 94.
- ↑ Wallis: A Beginner's Guide to Graph Theory. 2007, S. 126.
- ↑ Tittmann: Graphentheorie: Eine anwendungsorientierte Einführung. 2003, S. 61.
Weblinks
- Eric W. Weisstein: Star Graph. In: MathWorld (englisch).


















