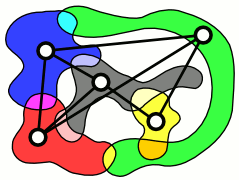
In der Graphentheorie ist ein Schnittgraph ein Graph, der die nicht-leeren Schnitte einer Familie von Mengen als Kanten darstellt. Jede Menge entspricht hierbei einem Knoten im Schnittgraphen. Für jedes Paar zweier Mengen in der Familie, die sich schneiden, hat der Schnittgraph eine Kante, umgekehrt besteht keine Kante zwischen zwei Mengen, wenn deren Schnitt die leere Menge ist.
Formale Definition
Formal ist ein Schnittgraph G ein ungerichteter Graph, der eine Familie von Mengen
darstellt, indem jede Menge mittels eines Knotens repräsentiert wird, und zwei Knoten und genau dann verbunden sind, wenn die Mengen, die sie repräsentieren, einen nicht-leeren Schnitt bilden, also
Literatur
- K. Čulík: Applications of graph theory to mathematical logic and linguistics. Theory of Graphs and its Applications (Proc. Sympos. Smolenice, 1963). Hrsg.: Publ. House Czechoslovak Acad. Sci. Prag 1964, S. 13–20.
Weitergehende Literatur
Eine Übersicht der Theorie für Schnittgraphen findet sich in McKee & McMorris (1999).
- McKee, Terry A.; McMorris, F. R. (1999), Topics in Intersection Graph Theory, SIAM Monographs on Discrete Mathematics and Applications, vol. 2, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 0-89871-430-3, MR 1672910.
Weblinks
- Jan Kratochvíl, A video lecture on intersection graphs (June 2007)
- E. Prisner, A Journey through Intersection Graph County





