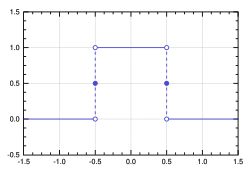
Die Rechteckfunktion, auch rect-Funktion, ist eine unstetige mathematische Funktion mit folgender Definition:

${\displaystyle \operatorname {rect} (t)=\Pi (t)={\begin{cases}0&{\text{wenn }}|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\text{wenn }}|t|={\frac {1}{2}}\\[3pt]1&{\text{wenn }}|t|<{\frac {1}{2}}\end{cases}}}$

Alternative Definitionen, die vor allem im Bereich der Signalverarbeitung üblich sind, legen die Rechteckfunktion vereinfacht fest als:^[1]

${\displaystyle \operatorname {rect_{d}} (t)={\begin{cases}1&{\text{wenn }}|t|\leq {\frac {1}{2}}\\[3pt]0&{\text{wenn }}|t|>{\frac {1}{2}}\end{cases}}}$

Die Rechteckfunktion kann auch mit Hilfe der Heaviside-Funktion ${\displaystyle \Theta (x)}$ ausgedrückt werden als:

${\displaystyle \operatorname {rect} (t)=\Theta \left(t+{\frac {1}{2}}\right)\cdot \Theta \left({\frac {1}{2}}-t\right)=\Theta \left(t+{\frac {1}{2}}\right)-\Theta \left(t-{\frac {1}{2}}\right)}$

Dabei ist ${\displaystyle \Theta (0)={\tfrac {1}{2}}}$ gesetzt.

Die Fourier-Transformation der Rechteckfunktion ergibt die sinc-Funktion ${\displaystyle \operatorname {sinc} (x)=\sin(\pi x)/(\pi x)}$:

${\displaystyle {\mathcal {F}}\{\operatorname {rect} (t)\}=\operatorname {sinc} (f)}$

Das gilt auch für ${\displaystyle \operatorname {rect_{d}} (t)}$. Umgekehrt gilt allerdings formal nicht

${\displaystyle {\mathcal {F}}\{\operatorname {sinc} (t)\}=\operatorname {rect} (f)}$.

Denn es ist ${\displaystyle \operatorname {sinc} \notin L^{1}(\mathbb {R} ^{n})}$, und somit konvergiert das Integral der gewöhnlichen Fouriertransformation nicht. Die Gleichung gilt allerdings im Sinne der Fouriertransformation temperierter Distributionen.

Eine Rechteckfunktion, die bei ${\displaystyle t_{0}}$ zentriert ist und eine Dauer von ${\displaystyle T}$ hat, wird ausgedrückt durch

${\displaystyle \operatorname {rect} \left({\frac {t-t_{0}}{T}}\right)\,.}$

Die Rechteckfunktion ist als unstetige Funktion weder im klassischen Sinne differenzierbar noch ist sie schwach differenzierbar. Allerdings ist eine Distributionenableitung durch die diracsche Delta-Distribution ${\displaystyle \delta }$ möglich:

${\displaystyle \operatorname {rect} '(t)=\delta \left(t+{\frac {1}{2}}\right)-\delta \left(t-{\frac {1}{2}}\right)}$

Die Faltung zweier gleicher Rechteckfunktionen ergibt die Dreiecksfunktion, die Integration eine Rampenfunktion. Eine Form mit periodischer Fortsetzung der Rechteckfunktion sind die Rademacherfunktionen. Eine weitere Form der periodischen Fortsetzung von ${\displaystyle \operatorname {rect} }$ ergibt die konstante Funktion ${\displaystyle \operatorname {1} }$.

Die mehrfache Faltung mit ${\displaystyle n\in \mathbb {N} }$ Faltungen

${\displaystyle \underbrace {\operatorname {rect} (t)*\operatorname {rect} (t)*\operatorname {rect} (t)*\dotsm } _{n{\text{-mal}}}}$

ergibt für ${\displaystyle n\to \infty }$ mit einer geeigneten Skalierung die Gaußsche Glockenkurve.

• Rechteckschwingung: Anwendung in der Signaltheorie und Elektrotechnik

• Eric W. Weisstein: Rectangle Function. In: MathWorld (englisch).

1. ↑ Hans Dieter Lüke: Signalübertragung. Grundlagen der digitalen und analogen Nachrichtenübertragungssysteme. 6., neubearbeitete und erweiterte Auflage. Springer, Berlin u. a. 1995, ISBN 3-540-58753-5, S. 2.