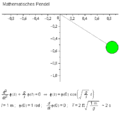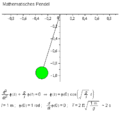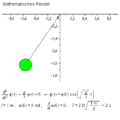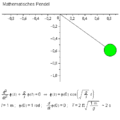
Ein Multipendel ist ein Pendel, an dessen Arm weitere Pendel gehängt sind. Es entsteht ein unvorhersehbares Bewegungsmuster, welches bereits bei geringfügigen Störungen stark variiert. Es lassen sich chaotische Prozesse leicht simulieren, weshalb es sich zu einem beliebten Modell in der Chaostheorie entwickelt hat.

Das Modell des Multipendels ${\displaystyle n}$-ter Stufe ist ein idealisiertes System eines Fadenpendels, an dessen schwingendem Massenpunkt ${\displaystyle n-1}$ weitere baugleiche Fadenpendel gekoppelt sind. Die verbindenden Fäden zwischen Aufhängepunkt und den Massenpunkten werden als vollkommen unelastische, massenlose Stäbe betrachtet. Das gesamte System wird als reibungsfrei aufgefasst.

Die Bewegungsgleichungen für ein Multipendel ${\displaystyle n}$-ter Stufe lassen sich mit dem Lagrange-Formalismus zweiter Art herleiten.

Mittels Trigonometrie erhält man:

${\displaystyle x_{1}=l_{1}\sin \varphi _{1}}$

${\displaystyle y_{1}=-l_{1}\cos \varphi _{1}}$

${\displaystyle x_{2}=l_{1}\sin \varphi _{1}+l_{2}\sin \varphi _{2}}$

${\displaystyle y_{2}=-l_{1}\cos \varphi _{1}-l_{2}\cos \varphi _{2}}$

...

${\displaystyle x_{n}=l_{1}\sin \varphi _{1}+...+l_{n}\sin \varphi _{n}}$

${\displaystyle y_{n}=-l_{1}\cos \varphi _{1}-...-l_{n}\cos \varphi _{n}}$

Folglich können die kartesischen Koordinaten ${\displaystyle (x_{k}|y_{k})}$ der Massenpunkte ${\displaystyle m_{k}}$ für ${\displaystyle k}$ ∈ {1,...,${\displaystyle n}$} und ihre zeitlichen Ableitungen in folgender Form geschrieben werden:

${\displaystyle x_{k}=\sum _{i=1}^{k}l_{i}\sin \varphi _{i}}$

${\displaystyle {\dot {x}}_{k}=\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\cos \varphi _{i}}$

${\displaystyle y_{k}=-\sum _{i=1}^{k}l_{i}\cos \varphi _{i}}$

${\displaystyle {\dot {y}}_{k}=\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\sin \varphi _{i}}$

Kinetische Energie ${\displaystyle T}$ und Potential ${\displaystyle V}$ ergeben:

${\displaystyle T(\varphi _{1},...,\varphi _{n},{\dot {\varphi }}_{1},...,{\dot {\varphi }}_{n})=\sum _{k=1}^{n}{\frac {m_{k}}{2}}({\dot {x}}_{k}^{2}+{\dot {y}}_{k}^{2})}$

${\displaystyle V(\varphi _{1},...,\varphi _{n})=g\sum _{k=1}^{n}m_{k}y_{k}}$

Somit ist die Lagrange-Funktion ${\displaystyle L=T-V}$:

${\displaystyle L(\varphi _{1},...,\varphi _{n},{\dot {\varphi }}_{1},...,{\dot {\varphi }}_{n})={\frac {1}{2}}\sum _{k=1}^{n}m_{k}\left[\left(\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\cos \varphi _{i}\right)^{2}+\left(\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\sin \varphi _{i}\right)^{2}\right]+g\sum _{k=1}^{n}\sum _{i=1}^{k}m_{k}l_{i}\cos \varphi _{i}}$

Die Bewegungsgleichungen des Multipendels n-ter Stufe ergeben sich aus

${\displaystyle {d \over dt}{\partial {L} \over \partial {{\dot {\varphi }}_{j}}}-{\partial {L} \over \partial {\varphi _{j}}}=0}$

bzw.

${\displaystyle {d \over dt}{\partial {T} \over \partial {{\dot {\varphi }}_{j}}}-{\partial {} \over \partial {\varphi _{j}}}(T-V)=0}$

für ${\displaystyle j}$ ∈ {1,...,${\displaystyle n}$}.

Die Bewegungsgleichungen für die generalisierten Koordinaten (${\displaystyle {\varphi _{1}},...,{\varphi _{n}}}$) stellen ein nichtlineares System von ${\displaystyle n}$ Differentialgleichungen zweiter Ordnung dar, welches für ${\displaystyle n>1}$ analytisch nicht lösbar ist.

Es kann bei ${\displaystyle 2n}$ bekannten Nebenbedingungen, beispielsweise den Startwerten

${\displaystyle \left(\varphi _{1}(t=0),...,\varphi _{n}(t=0),{\dot {\varphi }}_{1}(t=0),...,{\dot {\varphi }}_{n}(t=0)\right),}$

mittels numerischer Verfahren gelöst werden. Zwecks Vereinfachung der Bewegungsgleichungen können Kleinwinkelnäherungen vorgenommen werden.

Für Stufen ${\displaystyle n>1}$ entstehen chaotische Bewegungsmuster. Hier führen bereits geringfügige Änderungen der lokalen Koordinaten oder ihrer zeitlichen Ableitungen zu deutlichen Änderungen im weiteren Bewegungsablauf.

Für ${\displaystyle n=1}$ ergibt sich der einfache Fall des mathematischen Pendels.

Hier ergeben sich kinetische Energie ${\displaystyle T}$ und Potential ${\displaystyle V}$ zu

${\displaystyle T(\varphi ,{\dot {\varphi }})={\frac {m}{2}}l^{2}{\dot {\varphi }}^{2}}$

${\displaystyle V(\varphi )=-mgl\cos \varphi }$

mit ${\displaystyle m:=m_{1},l:=l_{1},\varphi :=\varphi _{1}}$.

Entsprechend ist die Bewegungsgleichung:

${\displaystyle {\ddot {\varphi }}+{\frac {g}{l}}\sin \varphi =0}$

Mit der Kleinwinkelnäherung ${\displaystyle \sin \varphi \approx \varphi }$ lässt sich die Gleichung vereinfachen:

${\displaystyle {\ddot {\varphi }}+{\frac {g}{l}}\varphi =0}$

Eine zweckmäßige Lösung der Bewegungsgleichung ist

${\displaystyle \varphi (t)=\varphi (0)\cos \left({\sqrt {\frac {g}{l}}}t+\alpha \right)}$,

sodass bei bekannten Startbedingungen für den Parameter ${\displaystyle \alpha }$ gilt:

${\displaystyle \alpha =\arcsin \left(-{\frac {{\dot {\varphi }}(0)}{\varphi (0)}}{\sqrt {\frac {l}{g}}}\right)}$

Das Pendel schwingt entsprechend harmonisch mit der Periode:

${\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}$

Der Fall ${\displaystyle n=2}$ stellt das Doppelpendel dar.

Hier ergeben sich kinetische Energie ${\displaystyle T}$ und Potential ${\displaystyle V}$ zu:

${\displaystyle T(\varphi _{1},\varphi _{2},{\dot {\varphi }}_{1},{\dot {\varphi }}_{2})={\frac {m_{1}}{2}}l_{1}^{2}{\dot {\varphi }}_{1}^{2}+{\frac {m_{2}}{2}}\left(l_{1}^{2}{\dot {\varphi }}_{1}^{2}+l_{2}^{2}{\dot {\varphi }}_{2}^{2}+2l_{1}l_{2}{\dot {\varphi }}_{1}{\dot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2})\right)}$

${\displaystyle V(\varphi _{1},\varphi _{2})=-(m_{1}+m_{2})gl_{1}\cos \varphi _{1}-m_{2}gl_{2}\cos \varphi _{2}}$

Entsprechend sind die Bewegungsgleichungen:

${\displaystyle m_{2}l_{2}{\ddot {\varphi }}_{2}\cos \left(\varphi _{1}-\varphi _{2}\right)+\left(m_{1}+m_{2}\right)l_{1}{\ddot {\varphi }}_{1}+m_{2}l_{2}{\dot {\varphi }}_{2}^{2}\sin \left(\varphi _{1}-\varphi _{2}\right)+\left(m_{1}+m_{2}\right)g\sin \varphi _{1}=0}$

und

${\displaystyle l_{2}{\ddot {\varphi }}_{2}+l_{1}{\ddot {\varphi }}_{1}\cos \left(\varphi _{1}-\varphi _{2}\right)-l_{1}{\dot {\varphi }}_{1}^{2}\sin \left(\varphi _{1}-\varphi _{2}\right)+g\sin \varphi _{2}=0}$

Ein Beispiel für ein Doppelpendel ist eine Glocke mit Klöppel.

Der Fall ${\displaystyle n=3}$ stellt das Tripelpendel dar.

Hier ergibt sich die kinetische Energie ${\displaystyle T}$ zu:

${\displaystyle T(\varphi _{1},\varphi _{2},\varphi _{3},{\dot {\varphi }}_{1},{\dot {\varphi }}_{2},{\dot {\varphi }}_{3})={\frac {m_{1}+m_{2}+m_{3}}{2}}l_{1}^{2}{\dot {\varphi }}_{1}^{2}+{\frac {m_{2}+m_{3}}{2}}l_{2}^{2}{\dot {\varphi }}_{2}^{2}+{\frac {m_{3}}{2}}l_{3}^{2}{\dot {\varphi }}_{3}^{2}+(m_{2}+m_{3})l_{1}l_{2}{\dot {\varphi }}_{1}{\dot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2})}$

${\displaystyle +m_{3}l_{1}l_{3}{\dot {\varphi }}_{1}{\dot {\varphi }}_{3}\cos(\varphi _{1}-\varphi _{3})+m_{3}l_{2}l_{3}{\dot {\varphi }}_{2}{\dot {\varphi }}_{3}\cos(\varphi _{2}-\varphi _{3})}$

Für das Potential ${\displaystyle V}$ gilt:

${\displaystyle V(\varphi _{1},\varphi _{2},\varphi _{3})=-(m_{1}+m_{2}+m_{3})gl_{1}\cos \varphi _{1}-(m_{2}+m_{3})gl_{2}\cos \varphi _{2}-m_{3}gl_{3}\cos \varphi _{3}}$

Entsprechend sind die Bewegungsgleichungen:

${\displaystyle m_{3}l_{3}{\ddot {\varphi }}_{3}\cos(\varphi _{1}-\varphi _{3})+(m_{2}+m_{3})l_{2}{\ddot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2})+(m_{1}+m_{2}+m_{3})l_{1}{\ddot {\varphi }}_{1}+m_{3}l_{3}{\dot {\varphi }}_{3}^{2}\sin(\varphi _{1}-\varphi _{3})}$

${\displaystyle +(m_{2}+m_{3})l_{2}{\dot {\varphi }}_{2}^{2}\sin(\varphi _{1}-\varphi _{2})+(m_{1}+m_{2}+m_{3})g\sin \varphi _{1}=0}$

und

${\displaystyle m_{3}l_{3}{\ddot {\varphi }}_{3}\cos(\varphi _{2}-\varphi _{3})+(m_{2}+m_{3})l_{2}{\ddot {\varphi }}_{2}+(m_{2}+m_{3})l_{1}{\ddot {\varphi }}_{1}\cos(\varphi _{1}-\varphi _{2})-(m_{2}+m_{3})l_{1}{\dot {\varphi }}_{1}^{2}\sin(\varphi _{1}-\varphi _{2})}$

${\displaystyle +m_{3}l_{3}{\dot {\varphi }}_{3}^{2}\sin(\varphi _{2}-\varphi _{3})+(m_{2}+m_{3})g\sin \varphi _{2}=0}$

und

${\displaystyle l_{3}{\ddot {\varphi }}_{3}+l_{2}{\ddot {\varphi }}_{2}\cos(\varphi _{2}-\varphi _{3})+l_{1}{\ddot {\varphi }}_{1}\cos(\varphi _{1}-\varphi _{3})-l_{2}{\dot {\varphi }}_{2}^{2}\sin(\varphi _{2}-\varphi _{3})-l_{1}{\dot {\varphi }}_{1}^{2}\sin(\varphi _{1}-\varphi _{3})+g\sin \varphi _{3}=0}$

• 
  Simulation: ${\displaystyle n=1}$
• 
  Simulation: ${\displaystyle n=2}$
• 
  Simulation: ${\displaystyle n=3}$

• Georg Hamel: Theoretische Mechanik. Springer, Berlin 1967. Berichtiger Reprint 1978, ISBN 3-540-03816-7
• Friedhelm Kuypers: Klassische Mechanik. 5. Auflage. VCH, Weinheim 1997, ISBN 3-527-29269-1
• Landau / Lifschitz: Lehrbuch der theoretischen Physik. Band 1: Mechanik. 14. Auflage. Deutsch, Thun 1997, ISBN 3-8171-1326-9

• Doppelpendel-Simulation in Java und Python

• L. D. Landau, E. M. Lifschitz: Volume 1 of Course of Theoretical Physics. 3rd Edition 1976, ISBN 0-7506-2896-0, §5, S. 11 f. (englisch)
• Herleitung der Differentialgleichungen zur Beschreibung des Doppelpendels (englisch)