Eine Hyperpyramide ist eine Verallgemeinerung des dreidimensionalen Pyramidenbegriffes auf n Dimensionen.

Bei einer dreidimensionalen Pyramide werden alle Eckpunkte eines (zweidimensionalen) Polygons in der Ebene, der Basis, mit einem Punkt im Raum, der Pyramidenspitze, verbunden. Diese Konstruktion wird nun bei der Hyperpyramide auf n Dimensionen erweitert. Die Basis, das heißt das Polygon in der Ebene, wird dabei zu einem (n-1)-Polytop in einer (n-1)-dimensionalen Hyperebene, dessen Eckpunkte man nun mit einem Punkt im n-dimensionalen Raum außerhalb der Hyperebene verbindet. Der so entstandene Körper wird als n-dimensionale Hyperpyramide bezeichnet. Der Abstand von der Pyramidenspitze zur Basis beziehungsweise zur Hyperebene, in der die Basis eingebettet ist, wird wie im dreidimensionalen Fall als Höhe bezeichnet.

Eine eindimensionale Hyperpyramide ist eine Strecke, eine zweidimensionale Hyperpyramide ein Dreieck und eine dreidimensionale Hyperpyramide die gewöhnliche Pyramide. Das Pentachoron ist eine vierdimensionale Hyperpyramide mit einem Tetraeder als Basis.

Das n-dimensionale Volumen einer n-dimensionalen Hyperpyramide beträgt:

${\displaystyle V_{n}={\frac {A\cdot h}{n}}}$

Hierbei bezeichnet ${\displaystyle V_{n}}$ das n-dimensionale Volumen der Hyperpyramide, A das (n-1)-dimensionale Volumen ihrer Basis und h ihre Höhe. Für die Fälle n=2 und n=3 liefert die obige Formel die bekannten Formeln für die Dreiecksfläche und das Pyramidenvolumen.

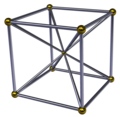
• Projektionen 4-dimensionaler Pyramiden verschiedener Basis
• 
  Tetraeder-Pyramide (Pentachoron)
• 
  Würfel-Pyramide
• 
  Oktaeder-Pyramide
• 
  Dodekaeder-Pyramide
• 
  Ikosaeder-Pyramide

Anmerkungen:

Darstellung als Schlegeldiagramm (dieses platziert die – eigentlich extradimensionale – Pyramidenspitze ins Zentrum).

Analog der Dualität von Würfel ↔ Oktaeder und Dodekaeder ↔ Ikosaeder sind auch die entsprechenden Pyramiden dual (die Tetraeder-Pyramide ist selbst-dual).

• A. M. Mathai: An Introduction to Geometrical Probability. CRC Press, 1999, ISBN 978-90-5699-681-9, S. 41–43 (Auszug (Google))
• M.G. Kendall: A Course in the Geometry of N Dimensions. Dover Courier, 2004 (Neuauflage), ISBN 978-0-486-43927-3, S. 37 (Auszug (Google))

• mathcurve.com