Eine Frontalperspektive ist in der Darstellenden Geometrie eine spezielle Art einer Zentralprojektion (Projektion eines Objektes mit von einem Punkt, dem Augpunkt, ausgehenden Strahlen auf eine Bildtafel), bei der wesentliche Teile des Objektes (z. B. eine Hausfront) in einer zur Bildtafel parallelen Ebene liegen. Geht man von drei zueinander senkrechten wesentlichen Richtungen (Länge, Breite und Höhe) des Objektes aus, so liefern nur die zur Bildtafel senkrechten Geraden, die sog. Tiefenlinien, einen Fluchtpunkt, und der ist gleich dem Hauptpunkt (s. Zentralprojektion). Deshalb wird eine Frontalperspektive auch Perspektive mit einem Fluchtpunkt genannt. In dem ersten Beispiel liegt die vordere Häuserfront sogar direkt in der Bildtafel und erscheint damit in der Frontalperspektive unverzerrt. Wäre die Häuserfront nur parallel und nicht in der Bildtafel, so wäre ihr Bild in der Frontalperspektive ein zum Original ähnliches (skaliertes) Bild. Die Stärke einer Frontalperspektive ist die Möglichkeit, einen vorhandenen Aufriss durch die Wahl eines geeigneten Hauptpunktes (Fluchtpunkt aller Tiefenlinien) zu einem räumlich wirkenden Bild zu ergänzen. Diese Verfahrensweise erinnert an die Anfertigung einer Kavaliersperspektive (s. Axonometrie). Eine Zweifluchtpunkt-Perspektive macht allerdings einen etwas harmonischeren Eindruck (s. Zentralprojektion), da sie nicht so sehr eine Seite des Objektes betont.

Anfertigung einer Frontalperspektive

Gegeben sind Grund- und Aufriss eines Hauses sowie Grund- und Aufriss des Augpunktes O. Die Bildtafel enthält die Vorderfront des Hauses (s. Vorgaben im zweiten Bild, links). Da wir den Aufriss in das perspektive Bild integrieren wollen, identifizieren wir als Hauptpunkt . Der Horizont verläuft horizontal (parallel zur Grundlinie der Hausfront = Standlinie) durch den Hauptpunkt. Die Projektionen aller Kanten, die senkrecht zur Hausfront verlaufen, haben H als Fluchtpunkt. Nun muss nur noch die Länge des Hauses (Abstand der Hinterfront von der Vorderfront) konstruiert werden. Hierfür verwenden wir einen der beiden Distanzpunkte auf dem Horizont. Es gibt zwei horizontale Geradenrichtungen, die mit der Bildtafel einen Winkel von einschließen. Ihre beiden Fluchtpunkte liegen links und rechts vom Hauptpunkt im Abstand d, der Distanz, und heißen deswegen Distanzpunkte. Wir verwenden den linken Distanzpunkt , um die Länge des Hauses von der Standlinie auf die entsprechende Hauskante der Seitenfront zu projizieren. Das Dreieck geht durch die Zentralprojektion in das Dreieck (s. Bild) über. Damit lässt sich die Frontalperspektive des Hauses vervollständigen.
Bemerkung: Die Distanzpunkte sind die Messpunkte der Tiefenlinien (s. Rekonstruktion).
Zwei weitere Beispiele
-
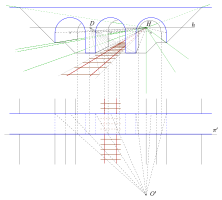
Frontalperspektive einer Brücke, Vorgabe
-
Frontalperspektive einer Brücke, Lösung




Im Beispiel der Frontalprojektion einer Brücke müssen Kreise projiziert werden. Ein Kreis kann bei einer Zentralprojektion in einen Kreis oder eine Ellipse oder eine Hyperbel oder eine Parabel oder eine Strecke übergehen. Die Fälle Hyperbel, Parabel, Strecke sind Sonderfälle und treten in der Regel selten auf. Aber auch der Fall „Bild ist eine Ellipse“ erfordert einige Mühe, da eine Zentralprojektion keine lineare Abbildung ist, d. h. z. B., dass der Kreismittelpunkt nicht in den Mittelpunkt der Bildellipse übergeht. All die großen Mühen bei der Abbildung von Kreisen lösen sich bei einer Frontalperspektive, bei der Kreise nur in der Bildtafel oder parallel dazu vorkommen (s. Brücke), in Wohlgefallen auf. Kreise in der Bildtafel werden unverzerrt und Kreise parallel zur Bildtafel werden in größere oder kleinere Kreise abgebildet. Dabei gehen Kreismittelpunkte in Kreismittelpunkte und Durchmesser in Durchmesser über. Auch beim Beispiel der Brücke wird der Aufriss zur Frontalprojektion ausgebaut. Die Abstände der Eisenbahnschwellen werden mit dem Distanzpunkt aus der Standlinie auf die zugehörige Tiefenlinie übertragen.
Die Frontalperspektive ist auch sehr gut geeignet Innenräume schnell und attraktiv darzustellen. Hierfür wählt man den Hauptpunkt H, die Standlinie s, eine Spur einer Seiten-Wand und eine gleichmäßige Unterteilung der Standlinie und dieser senkrechten Spur. Die Unterteilung dient dazu, ein Quadrat-Raster für den Fußboden und die seitlichen Wände zu erzeugen. Zunächst zeichnet man Verbindungen der Unterteilungspunkte auf der Standlinie/Spur mit dem Hauptpunkt. Dies ergibt die Längsgeraden des Rasters auf Fußboden und Seiten-Wände. Die Längsunterteilung erhält man durch Projektion der Unterteilung der Standlinie vom Distanzpunkt aus auf eine oder mehrere schon gezeichneten Längsgeraden (Tiefenlinien). Welchen Distanzpunkt (es gibt zwei: einer links und einer rechts des Hauptpunktes im Abstand der Distanz) man wählt, ist im Prinzip gleichgültig. Man sollte den Distanzpunkt wählen, der am wenigsten das Bild stört und am wenigsten „schleifende Schnitte“ liefert.
Literatur
- Fucke, Kirch, Nickel: Darstellende Geometrie. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4, S. 232–236
- Graf, Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9, S. 266.
Weblinks
- Darstellende Geometrie für Architekten (PDF; 1,5 MB). Skript (Uni Darmstadt), S. 96, 158, 197