Statische Bestimmtheit ist ein Begriff der Statik. Er charakterisiert die Lagerung ruhender Körper und den inneren Aufbau von Körpersystemen wie z. B. Fachwerke sowie die Lösbarkeit der mit ihr verbundenen Gleichgewichtsaufgabe mit den Mitteln der Starrkörpermechanik.^[1][2]

Lagerungen können grundsätzlich statisch bestimmt, unbestimmt oder überbestimmt sein. Die statische Bestimmtheit ist bei der Konzipierung von Konstruktionen von Bedeutung, vor allem in der Baustatik, in der Maschinentechnik und im Apparatebau. Statisch bestimmt gelagerte Körper bzw. statisch bestimmte Körpersysteme ertragen geometrische Einflüsse wie Wärmedehnungen, kleine Lagerverschiebungen, Herstellungs- und Montageungenauigkeiten usw. ohne Zwängungen und damit verbundene Kräfte, wie dies z. B. für Brücken und andere Tragwerke wesentlich sein kann.

Statisch bestimmt ist die Lagerung eines Körpers, wenn die unbekannten Lagerreaktionen (Kräfte und Momente) mit den Gleichgewichts-Bedingungen allein berechnet oder mit den Mitteln der graphischen Statik bestimmt werden können.^[3][4][5] Eine statisch bestimmte Lagerung ist bewegungsgeometrisch eindeutig und damit auch kinematisch bestimmt.^[3][6] Dies bedeutet, dass die Lagerung jeden der Bewegungsfreiheitsgrade des Körpers genau einmal einschränkt. Bei räumlichen Problemen sind es 6 Freiheitsgrade (je 3 Translationen und Rotationen), bei ebenen Problemen sind es 3 Freiheitsgrade (2 Translationen, 1 Rotation). Die einzelnen Lager tragen zu dieser entsprechend ihrer Wertigkeit mit Lagerreaktionen (Kräften und/oder Momenten) bei.^[6][7] Die Wertigkeit drückt die Anzahl Freiheitsgrade aus, die durch das betreffende Lager eingeschränkt werden. Jede Einschränkung eines Freiheitsgrades wird mathematisch durch eine entsprechende Gleichgewichtsbedingung ausgedrückt. Diese verknüpfen die als bekannt geltenden äußeren Belastungen (Kräfte und Momente) mit den unbekannten Lagerreaktionen und bilden ein lineares, homogenes Gleichungssystem. Statische Bestimmtheit verlangt als notwendige und hinreichende Bedingung, dass die Koeffizientenmatrix der unbekannten Lagerreaktionen quadratisch ist, und dass ihre Determinante ungleich Null ist. Dies trifft zu, wenn die Gleichgewichtsbedingungen voneinander linear unabhängig sind.^[3][7][8]

Schränkt die Lagerung einzelne Freiheitsgrade mehrfach ein, so enthält das Gleichungssystem mehr unbekannte Lagerreaktionen als Gleichgewichtsbedingungen; es ist mit letzteren allein nicht lösbar. Die Lagerung ist somit statisch unbestimmt^[9], aber wegen der Überzahl an bewegungsgeometrischen Bedingungen gleichzeitig auch geometrisch bzw. kinematisch überbestimmt.^[3][10] In solchen Fällen kann der Zusammenhang zwischen Belastung und Verformung des Körpers weitere Gleichungen liefern.^[6][10][11]

Aus einem statisch unbestimmt gelagerten Körper kann durch geeignete Unterteilung und Verbindung mittels Gelenken ein statisch bestimmtes Körpersystem erzeugt werden. Jedes eingefügte Gelenk erhöht den Freiheitsgrad bei ebenen Problemen um 1 bzw. bei räumlichen Problemen je nach Art des Gelenks um 1 bis 3. Einfache Beispiele hierfür sind der Gerberträger und der Dreigelenkbogen. Auch mit jedem plastischen Dreh- oder Verschiebungsgelenk wird der Grad der statischen Unbestimmtheit eines Körpers reduziert. Dies wird beim Traglastverfahren^[2] ausgenutzt, um die maximale Belastbarkeit eines Tragwerks bis zum Erreichen eines verschieblichen, also statisch überbestimmten Systems zu ermitteln.^[12]

Bei einer statisch unbestimmten Lagerung können die elastischen Bauteilverformungen reduziert werden, und eine Beeinträchtigung der Lagerung führt nicht zwingend zum vollständigen Funktionsausfall.^[12] Bei der Auslegung statisch unbestimmter Körper und Systeme sind die Beanspruchungen bzw. Zwängsspannungen zu berücksichtigen, die von geometrischen Einflüssen wie Wärmedehnungen, Schwindungen, kleinen Lagerverschiebungen, Herstellungs- und Montageungenauigkeiten usw. hervorgerufen werden.

Sind umgekehrt einzelne Freiheitsgrade nicht eingeschränkt, bestehen mehr Gleichgewichtsbedingungen als unbekannte statische Größen. Dann ist die Lagerung statisch überbestimmt bzw. kinematisch unbestimmt.^[6] In diesem Fall ist das Kräftegleichgewicht je nach den Gegebenheiten labil oder indifferent. Eine solche Situation liegt bei Bauteilen vor, deren Funktion eine bestimmte Beweglichkeit verlangt, z. B. die Rotation um die Körperachse bei einer Antriebswelle oder die freie Drehbarkeit eines Turmdrehkrans um die vertikale Achse bei Betriebsruhe, um das Schwenken in die Windrichtung zu ermöglichen. Ansonsten aber sind statisch überbestimmte, also verschiebliche Systeme für die Aufnahme statischer Kräfte ungeeignet.^[13][14]

In einfacheren Fällen kann mit technischem Sachverstand die statische Bestimmtheit durch eine qualitative, anschauliche Betrachtung beurteilt werden. Statisch bestimmte Konstruktionen lassen sich zwangsfrei zu einem unbeweglichen System aufbauen. Zur Beurteilung der statischen Bestimmtheit eines Körpers oder eines Körpersystems können auch geeignete Abzählformeln hilfreich sein. Zusätzlich zur statischen Bestimmtheit ist es sinnvoll, auch die technische Brauchbarkeit bzw. Tauglichkeit zu betrachten. Nicht jede statisch bestimmte Konstruktion ist zugleich brauchbar.

Um die Begriffe statisch unbestimmt und statisch überbestimmt bzw. kinematisch überbestimmt und kinematisch unbestimmt ist in jüngerer Zeit einige Verwirrung entstanden, indem sie entgegen ihrer klassischen Definition im deutschsprachigen Schrifttum vereinzelt auch umgekehrt^[15] oder vermischt gehandhabt werden.^[7]

Ein wichtiges Beurteilungskriterium ist der Grad der statischen Bestimmtheit^[16] bzw. etwas weniger allgemein Grad der statischen Unbestimmtheit^[13][14]. Er charakterisiert die Lagerung eines Körpers oder Körpersystems sowie dessen innerer Aufbau quantitativ. Diese ganzzahlige Kenngröße ${\displaystyle n}$ besteht beim einzelnen Körper aus der Differenz zwischen der Zahl ${\displaystyle r}$ unbekannter statischer Größen (Lagerreaktionen) und der Anzahl ${\displaystyle f}$ Gleichgewichtsbedingungen:

${\displaystyle n=r-f}$

Aus kinematischer Sicht bedeuten ${\displaystyle f}$ der Freiheitsgrad des frei beweglichen Körpers und ${\displaystyle r}$ die Anzahl konstruktionsseitig eingeschränkter Freiheitsgrade.

${\displaystyle n=0}$: statisch und kinematisch bestimmt, sofern jeder Freiheitsgrad genau einmal eingeschränkt ist,

${\displaystyle n>0}$: n-fach statisch unbestimmt bzw. kinematisch überbestimmt,

${\displaystyle n<0}$: n-fach statisch überbestimmt bzw. kinematisch unbestimmt, d. h. verschieblich.

In der Literatur wird die rechte Seite der obigen Formel und damit der Grad der statischen Bestimmtheit jedoch auch mit vertauschten Vorzeichen dargestellt.^[17]

Die Bedingung ${\displaystyle n=0}$ ist für die statische Bestimmtheit notwendig, aber nicht hinreichend. Denn es ist möglich, dass einzelne Freiheitsgrade nicht eingeschränkt sind, andere aber mehrfach. Dann ist die Koeffizientendeterminante der Gleichgewichtsbedingungen Null, und die Lagerung ist weder statisch noch kinematisch bestimmt. Jedes eingebaute einfache Gelenk erhöht den Freiheitsgrad um eine Rotation bei ebenen Problemen, um drei Rotationen bei räumlichen Problemen. Mit geeignet angebrachten Gelenken können statisch unbestimmte Probleme statisch bestimmt gemacht werden, wie z. B. beim Dreigelenkbogen oder beim Gelenkträger.

Die statische Bestimmtheit eines Systems, das aus mehreren, untereinander verbundenen Körpern besteht, z. B. ein Fachwerk, resultiert aus der Lagerung des Systems als Ganzes und aus seinem inneren Aufbau. Letzterer umfasst die einzelnen Teile des Systems wie Scheiben, Stäbe usw. sowie deren Verbindungen untereinander in Form von Knoten, Gelenken, Schiebehülsen und dgl.^[6] Die Lösbarkeit der Gleichgewichtsaufgabe des Systems setzt voraus, dass diese Verbindungen als reibungsfrei angenommen werden. Bei Körpersystemen ist zwischen der äußeren und der inneren statischen Bestimmtheit zu unterscheiden^[11]. Körpersysteme können äußerlich und innerlich statisch bestimmt oder unbestimmt sein. Ist ein System innerlich aber statisch überbestimmt bzw. kinematisch unbestimmt, wie z. B. ein Dreigelenkbogen, bedarf es für das eindeutige Kräftegleichgewicht einer entsprechend statisch unbestimmten äußeren Lagerung. Die statische Bestimmtheit eines Systems verlangt, dass die Summe von äußerer und innerer statischer Bestimmtheit ${\displaystyle n_{a}}$ bzw. ${\displaystyle n_{i}}$ verschwindet:

${\displaystyle n=n_{a}+n_{i}=0}$

Da diese Bedingung notwendig, aber nicht hinreichend ist, bedarf es für die Feststellung der statischen Bestimmtheit einer zusätzlichen Beurteilung des Systems. Ein äußerlich statisch unbestimmtes System kann insgesamt statisch bestimmt sein, wenn es entsprechend innerlich statisch überbestimmt ist. Ein System kann je nach Betriebszustand unterschiedliche statische Bestimmtheitsgrade annehmen, wie z. B. ein zweiachsiger Wagen auf horizontaler Unterlage. Sind beide Achsen fest gebremst, ist der Wagen äußerlich statisch unbestimmt, bei gelösten Bremsen ist er statisch überbestimmt. Statisch bestimmt ist er, wenn nur eine Achse fest gebremst ist.

Äußerlich statisch bestimmt ist das Körpersystem, wenn es nach dem Erstarrungsprinzip als Ganzes mit seiner Lagerung die Bedingungen der statischen Bestimmtheit wie ein Einzelkörper erfüllt (siehe oben).

Innerlich statisch bestimmt ist das Körpersystem, wenn es in sich selbst und ohne äußere Lagerung ein zwangsfrei aufbaubares, stabiles Ganzes bildet. Dann erfüllt jeder nach dem Zerlegungs- bzw. Schnittprinzip freigemachte, als starr betrachtete Teilkörper und jedes Verbindungsglied für sich die Gleichgewichtsbedingungen.^[11][13]

Der Grad der inneren statischen Bestimmtheit ergibt sich aus der Gesamtzahl ${\displaystyle s}$ an Stäben und der Gesamtzahl ${\displaystyle k}$ an Knoten für ebene Systeme aus der Beziehung

${\displaystyle n_{i}=3+s-2\cdot k}$

und für räumliche Systeme aus

${\displaystyle n_{i}=6+s-3\cdot k}$

Es handelt sich im Wesentlichen um den Vergleich der Anzahl ${\displaystyle s}$ unbekannter Stabkräfte mit der Anzahl Gleichgewichtsbedingungen an den ${\displaystyle k}$ Knoten, nämlich 2 pro Knoten in ebenen und 3 in räumlichen Systemen. ${\displaystyle n_{i}=0}$ ist das System innerlich statisch bestimmt, sofern es sich zwangsfrei zu einer unbeweglichen Konstruktion aufbauen lässt. Andernfalls liegt ein Grenz- oder Spezialfall vor.^[4] Bei ${\displaystyle n_{i}>0}$ ist es innerlich ${\displaystyle n_{i}}$-fach statisch unbestimmt, bei ${\displaystyle n_{i}<0}$ innerlich ${\displaystyle n_{i}}$-fach statisch überbestimmt. Letztere Systeme, die eine gewisse Verschieblichkeit aufweisen und für die reine Statik keine Bedeutung haben, werden auch etwa als Mechanismus bezeichnet.^[13]

Diese Abzählformeln sind aus den Bildungsgesetzen der Fachwerktheorie^[3] abgeleitet, gelten aber nicht nur für Fachwerke. Sie lassen sich auf beliebige Körpersysteme anwenden, wenn die einzelnen Teilkörper wie Scheiben oder Biegestäbe mit ihren Stabäquivalenten eingesetzt werden.^[13][17] Als Stabäquivalent wird die Anzahl an Stäben bezeichnet, die für den Ersatz des betreffenden Körpers durch ein innerlich statisch bestimmtes Stabwerk erforderlich sind.

Eine andere Betrachtungsweise vergleicht die Anzahl Gleichgewichtsbedingungen an den ${\displaystyle s}$ Stäben mit der Anzahl ${\displaystyle v}$ unbekannter Verbindungskräfte an den Knoten^[13] mit der Abzählformel

${\displaystyle n_{i}=3+v-3\cdot s}$

für ebene Systeme und

${\displaystyle n_{i}=6+v-6\cdot s}$ bzw. ${\displaystyle n_{i}=6+v-5\cdot s}$

für räumliche Systeme. Pro Stab gibt es 3 Gleichgewichtsbedingungen bei ebenen und 6 bei räumlichen Systemen, bzw. 5, wenn die Rotation der Stäbe um ihre eigene Achse entfällt. Zu beachten ist, dass Biegestäbe, Scheiben usw. wie Stäbe nur einfach gezählt werden. An einem Gelenkknoten treten bei der Verbindung zweier Stäbe bei ebenen Problemen 2, bei räumlichen Problemen 3 unbekannte Kraftkomponenten auf, pro weiteren angebundenen Stab kommen nochmal so viel dazu. Die Zahl ${\displaystyle v_{i}}$ unbekannter Verbindungskräfte (Wertigkeit) am ${\displaystyle i}$-ten Knoten mit ${\displaystyle q_{i}}$ gelenkig angebundenen Stäben beträgt damit ${\displaystyle v_{i}=2\cdot (q_{i}-1)}$ bei ebenen und ${\displaystyle v_{i}=3\cdot (q_{i}-1)}$ bei räumlichen Problemen.

Bei einem statisch unbestimmten System kann der Grad der statischen Bestimmtheit durch schrittweises Entfernen von Bindungen bzw. Anbringen virtueller Gelenke ermittelt werden, so dass ein statisch bestimmtes Grundsystem entsteht.^[16]

Umgekehrt kann man von einem statisch bestimmten Grundsystem ausgehen, wie z. B. einem Träger auf zwei Stützen, einem Kragarm, einem Dreigelenkrahmen, einem Fachwerk aus drei gelenkig miteinander verbundenen Stäben o. ä., und durch Ergänzen bzw. Entfernen von Bindungswertigkeiten/Lagerreaktionen das gewünschte System aufbauen.^[18]

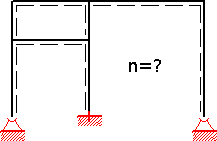
Beispiel: Bei einem System ist der Grad der statischen Unbestimmtheit gesucht. Es wird ein (ähnliches) statisch bestimmtes Grundsystem gewählt und anschließend statisch bestimmte Kragarme hinzugefügt. Man fügt Bindungen und Lagerreaktionen hinzu (bzw. bei kinematischen Systemen entfernt sie) und zählt ihre Wertigkeit zusammen.

• 
  Statisch unbestimmtes System mit Freiheitsgrad n > 0
• 
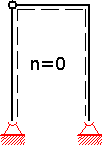
  Statisch bestimmtes Grundsystem
• 
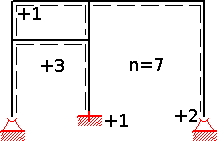
  Statisch bestimmtes Grundsystem mit Kragarmen
• 
  Man fügt 7 Lagewertigkeiten hinzu.

• N. Hinrichs: Keine Panik vor Mechanik! Springer, 2009, ISBN 978-3-8348-0646-8 (eingeschränkte Vorschau in der Google-Buchsuche). 
• C. Spura: Technische Mechanik 1. Stereostatik. Springer, 2016, ISBN 978-3-658-14984-0. 
• Karl-Eugen Kurrer: Geschichte der Baustatik. Auf der Suche nach dem Gleichgewicht, Ernst und Sohn, Berlin 2016, ISBN 978-3-433-03134-6, S. 32 ff.

1. ↑ Stephen P. Timoshenko, Donovan H. Young: Engineering Mechanics. 4th Ed. McGraw-Hill Kogakusha, Tokyo, 1956.
2. ↑ ^{a b} Karl-Eugen Kurrer: Geschichte der Baustatik. 2. Aufl. Wilhelm Ernst & Sohn Berlin, 2016.
3. ↑ ^{a b c d e} August Föppl: Vorlesungen über Technische Mechanik, Zweiter Band: Graphische Statik. Verlag von B. G. Teubner Leipzig, 1900.
4. ↑ ^{a b} Heinz Egerer: Ingenieur-Mechanik. Verlag von Julius Springer Berlin, 1919.
5. ↑ István Szabó: Einführung in die Technische Mechanik. 8. Aufl., Springer Verlag Berlin, 1975. S. 32.
6. ↑ ^{a b c d e} Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall: Technische Mechanik 1. 14. Aufl., Springer Verlag Berlin, 2019.
7. ↑ ^{a b c} Jürgen Dankert, Helga Dankert: Technische Mechanik – Statik, Festigkeitslehre, Kinematik/Kinetik. 7. Aufl., Springer Verlag Berlin, 2013.
8. ↑ Kurt Marguerre: Technische Mechanik, Erster Teil: Statik. Heidelberger Taschenbücher Band 20. Springer Verlag Berlin, 1967.
9. ↑ Beate Bender, Dietmar Gählich (Hrsg.): Dubbel Taschenbuch für den Maschinenbau 1: Grundlagen und Tabellen. 26. Aufl., Springer Vieweg Verlag Wiesbaden, 2020.
10. ↑ ^{a b} Wilhelm Flügge: Festigkeitslehre. Springer Verlag Berlin, 1967.
11. ↑ ^{a b c} Hans Ziegler: Mechanik I – Statik der starren und flüssigen Körper sowie Festigkeitslehre. 4. Aufl., Birkhäuser Verlag Basel und Stuttgart, 1962.
12. ↑ ^{a b} Johannes Winkler, Horst Aurich: Taschenbuch der Technischen Mechanik. 8. Aufl., Fachbuchverlag Leipzig im Carl Hanser Verlag München, 2006.
13. ↑ ^{a b c d e f} Hans Göldner: Leitfaden der Technischen Mechanik. 2. Aufl., VEB Fachbuchverlag Leipzig, 1967.
14. ↑ ^{a b} Bruno Assmann: Technische Mechanik, Band 1: Statik. 16. Aufl., Oldenbourg Verlag München Wien, 2002.
15. ↑ Peter Selke: Statik. De Gruyter Verlag Berlin, 2018.
16. ↑ ^{a b} Fritz Stüssi: Baustatik II. Springer Verlag Basel 1954.
17. ↑ ^{a b} Johannes Kunz: Statische Bestimmtheit – alles klar? Konstruktion 76(2024)6/7, S. 49–53
18. ↑ Bernhard Pichler, Josef Eberhardsteiner: Baustatik VO – LVA-Nr. 202.065. Hrsg.: E202 Institut für Mechanik der Werkstoffe und Strukturen – Fakultät Bauingenieurwesen, TU Wien. SS 2016 Auflage. TU Verlag, Wien 2016, ISBN 978-3-903024-17-5, Drehwinkelverfahren.